Download PDF of ICSE Class 10 Circles Previous Years’ Questions
ICSE Class 10 Circles Previous Years Questions + Solution
1. In the given figure, O is the centre of the circle. PQ is a tangent to the circle at T. Chord AB produced meets the tangent at P. AB = 9 cm, BP = 16 cm, ∠PTB = 50°, ∠OBA = 45°. Find:
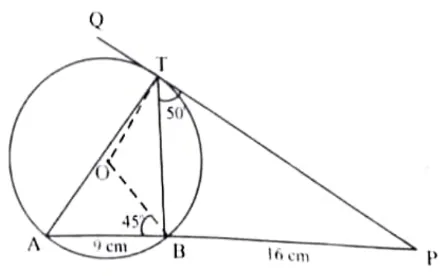
(a) length of PT
(b) ∠BAT
(c) ∠BOT
(d) ∠ABT [2023]
Answer: (a) 20cm (b) 50° (c) 100° (d) 85°
Step-by-step Explanation:
(a) We know, PT2 = AP x BP (When tangent and chord intersect externally, the product of the lengths of the segments of chord is equal to the square of the length of the tangent.)
PT2 =(16+9) x 16
PT2 =25 x 16
PT = √25×16
PT= 20 cm
(b) ∠BAT= ∠BTP = 50° (angle in the alternate segment)
(c) ∠BOT =2∠BAT= 100° (Angle subtended by an arc at the center of a circle is double the angle subtended by it on remaining part of the circle.)
(d) In ΔBOT, OB = OT (radii of a circle)
∴∠OBT=∠BTO= 180°-100°/2= 40°
∴∠ABT= 45° + 40°= 85°
Get the video solution of ICSE Class 10 Circles Previous Years Questions HERE.
2. In the given diagram RT is a tangent touching the circle at S. If ∠PST= 50° and ∠SPQ = 60° then ∠PSQ is equal to:

(a) 40°
(b) 30°
(c) 60°
(d) 90° [2023]
Answer: (d)
Step-by-step Explanation:
∠PQS=∠PST= 30°
In ΔPQS, ∠PQS +∠PSQ+∠QPS= 180°
∠PSQ= 180° – (60+30)°= 90°
3. In the given figure O, is the centre of the circle. CE is a tangent to the circle at A.
If ∠ABD=26°, then find

(a) ∠BDA
(b) ∠BAD
(c) ∠CAD
(d) ∠ODB [2023]
Answer: (a) 90° (b) 64° (c) 26° (d) 26°
Step-by-step Explanation:
(a) ∠BDA= 90° (angle in a semicircle is right angle.)
(b) ∠BAD= 180° – (90+26)° (sum of angles of a triangle is 180°
= 64°
(c) ∠CAD= 26° (angles in the alternate segments are equal.)
(d) ∠DOB= 2∠BAD= 2× 64= 128° (angle subtended by an arc at the center of a circle is double the angle subtended by it on any part on the remaining circle.)
∴ ∠ODB= 180° – (26+128)° =26° (sum of the angles of a triangle is 180°.)
4. In the given figure A, B, C and D are points on the circle with centre O. Given ∠ABC = 62°

Find:
(a) ∠ADC
(b) ∠CAB [2022 Semester-2]
Solution: (a) 62° (b) 28°
Step-by-step Explanation:
(a) ∠ADC= ∠ABC= 62° (Angles in the same segment are equal.)
(b) ∠ACB= 90° (angle in a semicircle is right angle.)
∴ ∠CAB= 180°– (62°+90°) =28° (sum of angles in a triangle is 180°.)
5. Two chords AB and CD of a circle intersect externally at E. If EC = 2 cm, EA = 3 cm and AB = 5 cm, Find the length of CD. [2022 Semester-2]

Answer: 10 cm
Step-by-step Explanation:
We know, AE × BE = CE × DE (when two chords intersect internally or externally, the products of the lengths of the segments of the chords are equal.)
3 × (3+5) = 2 × (2+CD)
24/2 = 2 + CD
10 = CD
CD = 10 cm
6. In the given figure O is the centre of the circle. PQ and PR are tangents and ∠QPR = 70°. Calculate

(a) ∠QOR
(b) ∠QSR [2022 Semester-2]
Answer: (a) 110° (b) 125°
Step-by-step Explanation:
(a) ∠PQO= ∠PRO = 90° (tangent and the radius of a circle through the point of contact are perpendicular to each other.)
In Quadrilateral PQOR,
∠RPQ +∠PQO +∠QOR + ∠PRO = 360°
70° + 90° +∠QOR + 90° = 360°
∠QOR = 360° – 250° = 110°
(b) reflex ∠QOR = 360°-110° = 250°
∠QSR = 125° (angle subtended by an arc at the center of a circle is double the angle subtended by it on any part on the remaining circle.)
ICSE Class 10 Maths PYQs chapter-wise
7. ABCD is a cyclic quadrilateral. If ∠BAD = (2x + 5)° and ∠BCD = (x + 10)° then x is equal to:
(a) 65° (b) 45° (c) 55° (d) 5° [2022 Semester-2]
Answer: (c)
Step-by-step Explanation:
We know, by theorem, opposite angles of a cyclic quadrilateral are supplementary.
∴ ∠BAD + ∠BCD = 180°
(2x + 5)° + (x + 10)° = 180°
3x +15 = 180
3x = 165
x = 55°
8. In the given figure TP and TQ are two tangents to the circle with centre O, touching at A and C, respectively. If ∠BCQ = 55° and ∠BAP = 60°, find:

(i) ∠OBA and ∠OBC
(ii) ∠AOC
(iii) ∠ATC [2020]
Answer: (i) 30°, 35° (ii) 130° (iii) 50°
Step-by-step Explanation:
(i) PAT and QCT are tangents to the circle.
∴ ∠QCO = ∠PAO = 90° (tangent and the radius of a circle through the point of contact are perpendicular to each other.)
Now, ∠BCQ = 55°.
∴ ∠BCO = 90 – 55 = 35°
In ΔBOC, OB = OC (radii)
∴ ∠OBC = ∠OCB = 35°
Similarly,
∠BAO = 90 – 60 = 30°
In ΔOAB, OA = OB (radii)
∴ ∠OBA = ∠BAO = 30°
(ii) ∠ABC= ∠OBA + ∠OBC = 30 + 35 = 65°
Hence, ∠AOC= 2∠ABC =130° (angle subtended by an arc at the center is double the angle subtended by it on the remaining part on the circle.)
(iii) ∠ATC= 360° – (∠TAO + ∠AOC + ∠TCO) (sum of angles of a quadrilateral is 360°.)
∴ ∠ATC= 360° – (90+130+90)°= 360°-310°= 50°
9. In the given figure AB = 9 cm, PA = 7.5 cm and PC = 5 cm. Chords AD and BC intersect at P.
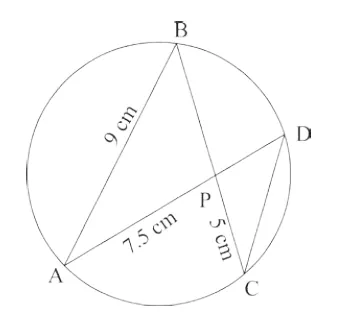
(i) Prove that ΔPAB ~ ΔPCD
(ii) Find the length of the CD.
(iii) Find area of ΔPAB : area of ΔPCD [2020]
Answer: (ii) 6 cm (iii) 9 : 4
Step-by-step Explanation:
(i) Chords AD and BC intersect internally. Therefore according to the theorem, the product of the lengths of their segments are equal.
∴ AP × PD = BP × PC
or, AP/PC = BP/PD
Now, In ΔPAB and ΔPCD
∠APB= ∠CPD (vertically opposite angles)
AP/PC = BP/PD (proved above)
∴ ΔPAB ~ ΔPCD (S-A-S condition of similarity)
(ii) As ΔPAB ~ ΔPCD
∴ AP/PC = BP/PD = AB/CD
AP/PC = AB/CD
7.5/5 = 9/CD
CD= 9/1.5= 6 cm
(iii) Area of ΔPAB : Area of ΔPCD = (PA/PC)2 (ratio of areas of similar triangles is equal to the square of the ratio of their corresponding sides.)
Area of ΔPAB : Area of ΔPCD = (7.5/5)2 =9 : 4
10. In the figure given below, O is the centre of the circle and AB is a diameter.
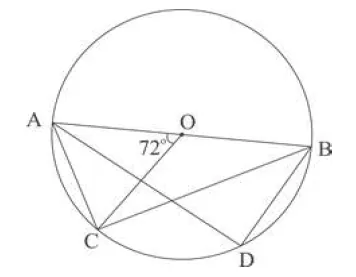
If AC = BD and ∠AOC = 72°. Find:
(i) ∠ABC
(ii) ∠BAD
(iii) ∠ABD [2020]
Answer: (i) 36° (ii) 36° (iii) 54°
Step-by-step Explanation:
(i) ∠ABC = 1/2∠AOC =36° (angle subtended by an arc at the center is double the angle subtended by it on the remaining part on the circle.)
(ii) ∠BAD= ∠ABC = 36° (equal chords subtend equal angles.)
(iii) ∠ADB= 90° (angle in a semicircle is right angle.)
∴ ∠ABD= 180°- (∠BAD + ∠ADB) (sum of angles of a triangle is 180°.)
or, ∠ABD= 180° – 126°= 54°
11. In the given figure, AC is a tangent to the circle with center 0. If ∠ADB = 55°, find x and y. Give reasons for your answers. [3] [2019]
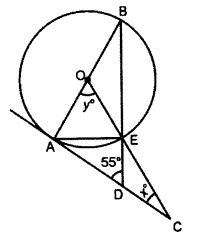
Answer: x= 20° , y= 70°
Step-by-step Explanation:
∠AEB= 90° (angle in a semicircle is right angle.)
∴ ∠AED= 90° (linear pair)
∠DAE= 180°-(90°+55°)= 35°
∴∠ABE= 35° (angles in the alternate segments are equal.)
∴ ∠AOE= y°= 70° (angle subtended by an arc at the center is double the angle subtended by it on the remaining part on the circle.)
∠OEB=∠OBE= 35° (isosceles triangle property)
Hence, ∠DEC=∠OEB= 35°
∠EDC= 180 – 55=125° (linear pair)
Hence, x°= 180° – (125 + 35)° = 20°
12. In the given figure, ABCDE is a pentagon inscribed in a circle such that AC is a diameter and side BC || AE. If ∆BAC = 50°, find giving reasons : [4]
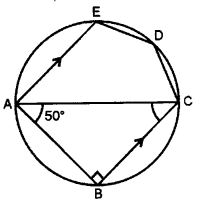
(i) ∠ACB
(ii) ∠EDC
(iii) ∠BEC [2019]
Answer: (i) 40° (ii) 140° (iii) 50°
Step-by-step Explanation:
(i) ∠ABC= 90° (angle in a semicircle is right angle.)
Hence, ∠ACB= 180° – (90+50)°= 40°
(ii) ∠CAE=∠ACB= 40°
Hence, ∠EDC= 180° – 40°= 140° (opposite angles of a cyclic quadrilateral are supplementary.)
(iii) ∠BEC= ∠BAC= 50° (angles in the same segment are equal.)
13. PQRS is a cyclic quadrilateral. Given ∠QPS = 73°, ∠PQS = 55° and ∠PSR = 82°, calculate: [4]

(i) ∠QRS
(ii) ∠RQS
(iii) ∠PRQ [2018]
Answer: (i) 107° (ii) 43° (iii) 52°
Step-by-step Explanation:
(i) ∠QRS= 180°- 73° = 107° (opposite angles of a cyclic quadrilateral are supplementary.)
(ii) ∠PSQ= 180° – (73 +55)°=52°
∴ ∠RSQ= 82 – 52= 30°
Hence, ∠RQS= 180°- (107 + 30)°= 43°
(iii) ∠PRQ= ∠PSQ= 52° (angles in the same segment are equal.)
14. In the figure given below ‘O’ is the center of the circle. If QR = OP and ∠ORP= 20°. Find the value of ‘x ’ giving reasons. [3] [2018]

Answer: 60°
Step-by-step Explanation:
OP=QR (given) and OP= OQ (radii)
Hence, OQ = QR
∴ ∠QOR =∠ORQ= 20°
∴ ∠OQR= 180° – 40°= 140° (angle sum property of triangle)
∴ ∠OQP= 180° – 140° =40°
∴ ∠OPQ= 40°
∴ ∠POQ= 180° – 80° = 100°
∴ x°= 180°- (100 +20)° = 60° (angles in a straight line)
15. AB and CD are two parallel chords of a circle such that AB = 24 cm and CD = 10 cm. If the radius of the circle is 13 cm, find the distance between the two chords. [3] [2017]

Answer: 17 cm
Step-by-step Explanation:
Join OB and OD,
NB= 1/2 AB= 12 cm and MD= 1/2 CD= 5 cm (perpendicular drawn from the center of a circle to the chord bisects it.)
In ΔONB, By pythagoras theorem,
ON = √OB2 -NB2
ON = √169 – 144 = 5 cm
In ΔOMD, By pythagoras theorem,
OM = √OD2 – MD2
ON = √169 – 25 = 12 cm
∴ MN= 5 + 12= 17 cm
16. In the given figure PQ is a tangent to the circle at A. AB and AD are bisectors of ∠CAQ and ∠PAC. If ∠BAQ = 30° prove that :
(i) BD is a diameter of the circle.
(ii) ABC is an isosceles triangle. [2017]

Step-by-step Explanation:
(i) Given that AB and AD are bisectors of ∠CAQ and ∠PAC.
Let ∠CAB= ∠BAQ= x° and ∠CAD= ∠DAP= y°.
∴ ∠BAQ +∠CAB +∠CAD +∠DAP= (2x + 2y)°
(2x + 2y)°= 180° (angles in a straight line.)
2(x+y) = 180°
x + y = 90°
or, ∠BAD = 90°
Hence, BD is the diameter of the circle. (angle in a semicircle is right angle.)
(ii) ∠ACB = ∠BAQ = x° (angles in the alternate segments are equal.)
∠CAB = x°
∴ AB = BC
Hence, ABC is an isosceles triangle.
Get the video solution of ICSE Class 10 Circles Previous Years Questions HERE.
17. In the figure given, O is the center of the circle. ∠DAE = 70°. Find giving suitable reasons, the measure of: [4]
(i) ∠BCD
(ii) ∠BOD
(iii) ∠OBD [2017]
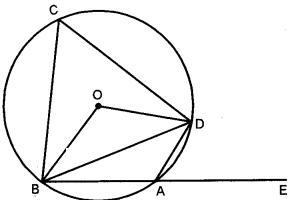
Answer: (i) 70° (ii) 140° (iii) 20°
Step-by-step Explanation:
(i) ∠BCD = ∠DAE = 70° (exterior angle of a cyclic quadrilateral is equal to opposite interior angle.)
(ii) ∠BOD = 2∠BCD = 140° (angle subtended by an arc at the center is double the angle subtended by it on the remaining part on the circle.)
(iii) In ΔBOD, OB = OD (radii)
∴ ∠OBD = ∠ODB = 180 – ∠BOD / 2 = 20°
18. In the given figure below, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.
Find :
(i) ∠OBD
(ii) ∠AOB
(iii) ∠BED [4] [2016]
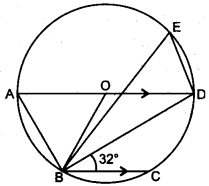
Answer: (i) 32° (ii) 64° (iii) 58°
Step-by-step Explanation:
(i) Since AD is parallel to BC,
∠ODB = ∠CBD = 32° (alternate interior angles)
∠OBD =∠ODB = 32° (property of isosceles triangle.)
(ii) ∠AOB = 2∠ODB = 64° (angle subtended by an arc at the center is double the angle subtended by it on the remaining part on the circle.)
(iii) ∠BOD = 180° – ∠AOB = 180° – 64° = 116°
Hence, ∠BED = 116/2 = 58° (angle subtended by an arc at the center is double the angle subtended by it on the remaining part on the circle.)
19. In the figure given below, O is the centre of the circle and SP is a tangent. If ∠SRT = 65°, find the value of x, y and z. [4] [2015]

Answer: x=25°, y= 50°, z= 40°
Step-by-step Explanation:
∠RST= 90° (tangent and the radius of a circle through the point of contact are perpendicular to each other.)
Hence, ∠RTS= x= 180° – (65 + 90)°= 25°
y = ∠SOQ= 2∠RST= 50° (angle subtended by an arc at the center is double the angle subtended by it on the remaining part on the circle.)
z= ∠OPS= 180° – (90 + 50)°= 40°
20. AB and CD are two chords of a circle intersecting at P. Prove that AP × PB = CP × PD. [3] [2015]
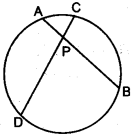
Step-by-step Explanation:

Let us join AD and BC.
Now, In ΔAPD and ΔCPB,
∠A =∠C (angles in the same segment are equal.)
∠APD = ∠BPC (vertically opposite angles)
∴ ΔAPD ~ ΔCPB (A-A condition of similarity)
∴ AP/CP = PD/PB
or, AP × PB = CP × PD
Proved.
21. In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate: [3]
(i) ∠BDC
(ii) ∠BEC
(iii) ∠BAC [2014]
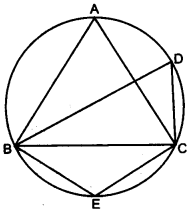
Answer: (i) 32° (ii) 148° (iii) 32°
Step-by-step Explanation:
(i) ∠BCD= 90° (angle in a semicircle is right angle.)
∴ ∠BDC= 180°– (∠BCD + ∠DBC)
=180° – (90 + 58)°
= 180° – 148° = 32°
(ii) ∠BEC = 180° – ∠BDC = 180° – 32°= 148° (opposite angles of a cyclic quadrilateral are supplementary.)
(iii) ∠BAC = ∠BDC = 32° (angles in the same segment are equal.)
22. In the figure given below, diameter AB and CD of a circle meet at P. PT is a tangent to the circle at T. CD=7.8 cm, PD=5 cm, PB=4 cm.

Find:
(i) AB.
(ii) the length of tangent PT. [3][2014]
Answer: (i) 12 cm (ii) 8 cm
Step-by-step Explanation:
(i) We know, When two chords intersect internally or externally, the product of the lengths of the segments of the chords are equal.
∴ AP × PB = CP × PD
or, (AB +4) × 4 = (7.8 + 5) × 5
or, AB + 4 = 12.8 × 5/4
or, AB = 16 – 4 = 12 cm
(ii) We know, When a tangent and a chord of a circle intersect externally, the product of the lengths of the segments of the chord is equal to the square of the length of the tangent.
∴ PT2 = AP × PB
or, PT2 = 16× 4
or, PT = √64
PT = 8
23. In the figure given below, O is the centre of the circle. AB and CD are two chords of the circle. OM is perpendicular to AB and ON is perpendicular to CD. AB = 24 cm, OM = 5 cm, ON = 12 cm.
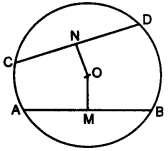
Find the :
(i) radius of the circle.
(ii) length of chord CD. [3] [2014]
Answer: (i) 13 cm (ii) 10 cm
Step-by-step Explanation:
Let us join CO and AO.
(i) In ΔAMO, AM = 24/2 = 12 cm. (Perpendicular drawn from the centre of a circle to the chord bisects it.)
∴ by pythagoras theorem,
AO = √AM2 + OM2
AO = √122 + 52
AO = √169 = 13 cm
∴ radius = 13 cm
(ii) In ΔCNO,
CN = √CO2 – ON2
CN = √132 – 122
CN = √25 = 5 cm
∴ CD = 2 CN = 10 cm
24. In the given figure,
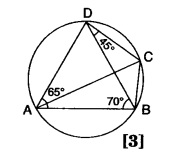
∠BAD = 65°,
∠ABD = 70°,
∠BDC = 45°
i.)Prove that AC is a diameter of the circle.
ii.)Find ∠ACB. [2013]
Answer: (ii) 45°
Step-by-step Explanation:
(i) In ΔADB,
∠ADB = 180°- (65+70)°= 45°
∴∠ADC = (45+45)°= 90°
Hence, AC is the diameter of the circle. (angle in a semicircle is a right angle.)
(ii) ∠ACB =∠ADB = 45°
25. In the given circle with centre O, ∠ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C.
Find ∠ADC and ∠DCT. [2013]

Answer: ∠ADC = 80° and ∠DCT= 60°
Step-by-step Explanation:
∠ADC= 180°-∠ABC (opposite angles of a cyclic quadrilateral are supplementary.)
∠ADC= (180-100)° = 80°
∠DAC= 180°-(40 + 80)° = 60°
∴∠DCT = ∠DAC= 60° (angles in the alternate segment are equal.)
26. In the given figure O is the centre of the circle and AB is a tangent at B. If AB = 15 cm and AC = 7.5 cm. Calculate the radius of the circle. [3] [2012]

Answer: 11.25 cm
Step-by-step Explanation:
We know, When a tangent and a chord of a circle intersect externally, the product of the lengths of the segments of the chord is equal to the square of the length of the tangent.
∴ AB2 = AC × AD
or, 152 = 7.5 × (CD + 7.5)
or, CD + 7.5 = 225/7.5
or, CD = 30 – 7.5 = 22.5 cm
CD is the diameter of the circle.
∴ radius= 22.5/2= 11.25 cm
27. In the given figure AB is the diameter of a circle with centre O. ∠BCD = 130°. Find:
(i) ∠DAB
(ii) ∠DBA. [3] [2012]
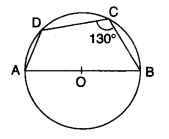
Answer: (i) ∠DAB=50° (ii) ∠DBA= 40°
Step-by-step Explanation:
(i) ∠DAB= 180°-130°= 50° (opposite angles of a cyclic quadrilateral are supplementary.)
(i) ∠ADB= 90° (angle in a semicircle is right angle.)
∴ In ΔADB,
∠DBA= 180°- (90+50)°=40°
28. In triangle PQR, PQ = 24 cm, QR = 7 cm and ∠PQR = 90°. Find the radius of the inscribed circle. [2012]

Answer: 3cm
Step-by-step Explantion:
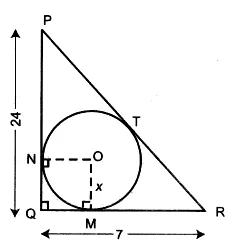
PR2 =QR2 + PQ2
PR2 = 72 + 242
PR= √625 = 25 cm
ON and OM are joined.
We know, tangent to a circle and radius through the point of contact are perpendicular to each other.
∴ ∠ONQ= 90° and ∠OMQ= 90°
QM = QN (tangents drwan from an external point to a circle are equal in length.)
∴ OMQN is a square with each side x cm.
∴ MR= TR=(7-x) cm, PN=PT= (24-x) cm
Now, PR= PT + TR
(24-x) + (7-x) = 25
or, 31 – 2x = 25
or, 2x = 6
or, x= 3 cm
Hence, radius= 3cm
29. In the given figure O is the centre of the circle. Tangents at A and B meet at C. If ∠AOC = 30°, find
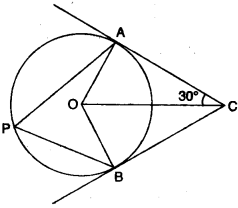
(i) ∠BCO
(ii) ∠AOB
(iii) ∠APB [3] [2011]
Answer: (i) 30° (ii) 120° (iii) 60°
Step-by-step Explanation:
(i) ∠BCO = ∠ACO = 30° (two tangents drawn from an external point to a circle are equally inclined to the line segment joining the centre to that point.)
(ii) ∠OAC = ∠OBC = 90° (tangent to a circle and radius through the point of contact are perpendicular to each other.)
∴ ∠AOB = 360°- (90 +30 + 30 +90)° = 120°
(iii) ∠APB = 1/2 of ∠AOB = 1/2 of 120°= 60°
30. ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles. [3][2011]
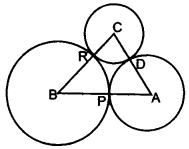
Answer: 6 cm, 2 cm, 4 cm
Step-by-step Explanation:
Let the radii of the three circles be r1 , r2 , and r3 respectively.
so, BC= r1 + r2 = 8 …… (1)
AC= r2 + r3 = 6 ….. (2)
AB= r1 + r3 = 10 ….. (3)
Adding (1), (2) and (3) we get,
2( r1 + r2 + r3)= 24
r1 + r2 + r3 =12 …. (4)
subtracting (1) from (4), we get,
(r1 + r2 + r3)-(r1 + r2)=12- 8
r3 =4 cm
Similarly, subtracting (2) from (4), we get,
r1 = 6 cm and
subtracting (3) from (4), we get,
r2 = 2 cm
31. In the following figure O is the centre of the circle and AB is a tangent to it at point B. ∠BDC = 65°. Find ∠BAO. [3] [2010]
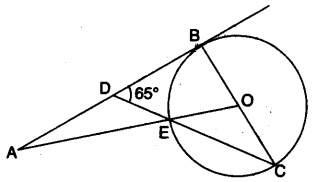
Answer: 40°
Step-by-step Explanation:
In ΔCBD, ∠ABO= 90° (tangent to a circle and radius through the point of contact are perpendicular to each other.)
∴ ∠BCD= 180°-(65 + 90)°= 25°
∴ ∠BOA= 2∠BCD= 50° (angle subtended by an arc at the centre of a circle is double the angle subtended by it on the remaining part of the circle.)
In ΔAOB, ∠BAO= 180°-(90 + 50)°= 40°
ICSE Related Links
Chapter-wise Quiz/MCQ/Test:
ICSE Chapter wise Quiz For Class 6
ICSE Chapter wise Quiz For Class 7
ICSE Chapter wise Quiz For Class 8
ICSE Chapter wise Quiz For Class 9
ICSE Chapter wise Quiz For Class 10
Sample Papers
Board Papers
ICSE Class 9 Board Exam Papers
ICSE Class 10 Board Exam Papers
CBSE Related Links
Chapter wise Quiz/MCQ/Test
CBSE Chapter-wise Quiz for Class 6
CBSE Chapter-wise Quiz for Class 7
CBSE Chapter-wise Quiz for Class 8
CBSE Chapter-wise Quiz for Class 9
CBSE Chapter-wise Quiz for Class 10
Sample Papers
Board Papers
CBSE Class 10 Previous years’ Board Papers
Subscribe to our channel for more such educational updates.

