Download PDF of ICSE Class 10 Similarity Previous Years Questions
ICSE Class 10 Similarity Previous Years Questions+Solution
1. In the given figure, AC ∥ DE ∥ BF. If AC = 24 cm, EG = 8 cm, GB = 16 cm, BF = 30 cm,
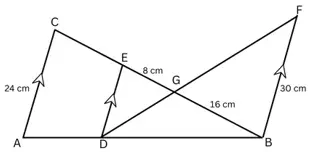
(a) prove ΔGED ~ ΔGBF
(b) find DE.
(c) DB : AB
Solution: (b) 15 cm (c) 5 : 8
Step-by-step Explanation:
(a) In ΔGED and ΔGBF,
∠EGD = ∠BGF (vertically opposite angles)
∠GED = ∠GBF (alternate interior angles)
∴ ΔGED ~ ΔGBF (by A-A axiom of similarity)
(b) as ΔGED ~ ΔGBF
∴ GE/BG = DE/BF = DG/GF
GE/BG = DE/BF
8/16 = DE/30
DE = 8×30/16
DE = 15 cm
(c) In ΔDBE and ΔABC,
∠B = ∠B (common)
∠EDB = ∠CAB (corresponding angles)
∴ ΔDBE ~ ΔABC (by A-A condition of similarity)
∴ DB/AB = BE/BC = DE/AC
DB/AB = DE/AC
DB/AB = 15/24 = 5/8
DB : AB = 5 : 8
2. In the given figure, ∠BAP = ∠DCP = 70°, PC = 6 cm and CA = 4 cm, then PD : DB is
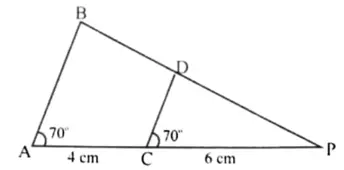
(a) 5 : 3
(b) 3 : 5
(c) 3 : 2
(d) 2 : 3 [2023]
Solution: (c) 3 : 2
Step-by-step Explanation:
In ΔPCD and ΔPAB,
∠PCD = ∠BAP = 70°, (given)
∠DPC = ∠BPA (common)
∴ ΔPCD ~ ΔPAB (by A-A condition of similarity)
∴ PC/PA = PD/PB = CD/AB
PC/PA = PD/PB
6/6+4 = 6/10 = 3/5 = PD/PB
As PD : PB = 3 : 5, therefore PD : DB = 3 : (5-3) = 3 : 2
option (c) is correct.
ICSE Class 10 Maths PYQs chapter-wise
3. In the given figure, PQ is parallel to TR, then by using condition of similarity:
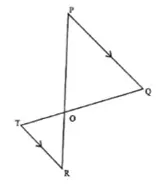
(a) PQ/RT = OP/OT = OQ/OR
(b) PQ/RT = OP/OR = OQ/OT
(c) PQ/RT = OR/OP = OQ/OT
(d) PQ/RT = OP/OR = OT/OQ
[2021 SEMESTER-1]
Solution: (b) PQ/RT = OP/OR = OQ/OT
Step-by-step Explanation:
In ΔPOQ and ΔROT,
∠POQ = ∠ROT (vertically opposite angles)
∠OPQ = ∠ORT (alternate interior angles)
∴ ΔPOQ ~ ΔROT (by A-A condition of similarity)
so, PQ/RT = OP/OR = OQ/OT
Video solution of ICSE Class 10 Similarity Previous Years Questions
4. In the given figure ABCD is a trapezium in which DC is parallel to AB. AB = 16 cm and DC = 8 cm. OD = 5 cm, OB = (y + 3) cm, OA = 11 cm and OC = (x – 1) cm. Using the given information answer the following questions. [2021 Semester-I]
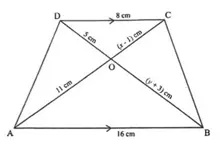
(i.) From the given figure name the pair of similar triangles:
(a) ∆OAB, ∆OBC (b) ∆COD, ∆AOB (c) ∆ADB, ∆ACB (d) ∆COD, ∆COB
(ii.) The corresponding proportional sides with respect to the pair of similar triangles obtained in (i):
(a) CD/AB = OC/OA = OD/OB (b) AD/BC = OC/OA = OD/OB
(c) AD/BC = BD/AC = AB/DC (d)OD/OB = CD/CB = OC/OA
(iii.) The ratio of the sides of the pair of similar triangles is:
(a) 1 : 3 (b) 1 : 2 (c) 2 : 3 (d) 3 : 1
(iv.) Using the ratio of sides of the pair of similar triangles values of x and y are respectively:
(a) x = 4.6, y = 7 (b) x = 7, y = 7 (c) x = 6.5, y = 7 (d) x = 6.5, y = 2
Solution: (i) (b) (ii) (a) (iii) (b) (iv) (c)
Step-by-step Explanation:
In ΔCOD and ΔAOB,
∠COD = ∠AOB (vertically opposite angles)
∠OCD = ∠OAB (alternate interior angles)
∠POQ = ∠ROT (vertically opposite angles)
∴ ΔCOD ~ ΔAOB (by A-A condition of similarity)
Option (b) is correct.
(ii) Therefore, CD/AB = OC/OA = OD/OB
option (a) is correct.
(iii) CD/AB = 8/16 = 1 : 2
option (b) is correct.
(iv) We know, CD/AB = OC/OA = OD/OB
CD/AB = OC/OA
1/2 = x-1/11
2(x-1) = 11
2x-2 = 11
2x = 11+2
x = 13/2 = 6.5 cm
Now, CD/AB = OD/OB
1/2 = 5/y+3
y+3 = 10
y = 7
option (c) is correct.
5. In the given figure, AB = 24 cm, AC = 18 cm, DE = 12cm, DF = 9 cm and ∠BAC = ∠EDF. Then ΔABC ~ ΔDEF by the condition:
(a) AAA
(b) SAS
(c) SSS
(d) AAS [2021 Semester-1]
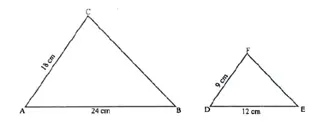
Solution: (b)
Step-by-step Explanation:
In ΔABC and ΔDEF,
AC/DF = 18/9 =2/1
∠BAC = ∠EDF (given)
AB/DE = 24/12 = 2/1
∴ ΔABC ~ ΔDEF (by S-A-S condition of similarity)
option (b) is correct.
6. In the given figure, ∠PQR = ∠PST = 90°, PQ = 5 cm and PS = 2 cm.
(i) Prove that △PQR ∼ △PST.
(ii) Find Area of △PQR: Area of quadrilateral SRQT. [2019]
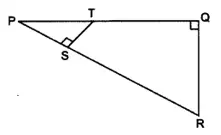
Solution: (ii) 25 : 21
Step-by-step Explanation:
(i) In ΔPQR and △PST,
∠P is common.
∠PQR= ∠PST = 90° (given)
∴ ΔPQR ~ ΔPST (A-A condition of similarity)
(ii) ∴ PQ/PS = QR/ST = PR/PT
As ΔPQR ~ ΔPST, therefore
Area of ΔPQR / Area of ΔPST =(PQ/PS)2 =(5/2)2 =25 : 4
∴ Area of ΔPQR / Area of quadrilateral SRQT = Area of ΔPQR / Area of ΔPQR-area of ΔPST
=25/25-4 = 25/21 = 25 : 21
7. In ∆ PQR, MN is parallel to QR and PM/MQ = 2/3 [3]
(i) Find MN / QR
(ii) Prove that ∆OMN and ∆ORQ are similar.
(iii) Find, Area of ∆OMN: Area of ∆ORQ [2018]
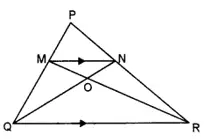
Solution: (i) 2/5 (iii) 4 : 25
Step-by-step Explanation:
(i) In ΔPMN and △PQR,
∠P is common.
∠PMN= ∠PQR (corresponding angles)
∴ ΔPMN ~ ΔPQR (A-A condition of similarity)
We know, PM/MQ = 2/3
∴ PM/PQ = PM/PM + MQ = 2/2+3 = 2/5
∴ PM/PQ = MN/QR = PN/PR = 2/5
∴ MN/QR = 2/5
(ii) In ΔOMN and △ORQ,
∠MON = ∠ROQ (vertically opposite angles)
∠OMN= ∠ORQ (alternate interior angles)
∴ ΔOMN ~ ΔORQ (A-A condition of similarity)
(iii) Area of ΔOMN / Area of ΔORQ =(MN/QR)2 =(2/5)2 = 4 : 25
8. PQR is a triangle. S is a point on the side QR of ∆PQR such that ∠PSR = ∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm.
(i) Prove ∆PQR ~ ∆SPR
(ii) Find the length of QR and PS
(iii) area of ΔPQR/ area of ΔSPR [2017]
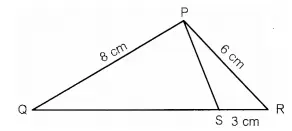
Solution: (ii) OR=12cm, PS = 4cm (iii) 4 : 1
Step-by-step Explanation:
(i) In ΔPQR and △SPR,
∠R is common.
∠PSR = ∠QPR (given)
∴ ΔPQR ~ ΔSPR (A-A condition of similarity)
(ii) ∴ PQ/PS = QR/PR = PR/SR
PQ/PS = PR/SR
8/PS = 6/3
PS = 4 cm
QR/PR = PR/SR
QR/6 = 6/3
QR = 12 cm
(iii) Area of ΔPQR / Area of ΔSPR =(PR/SR)2 =(6/3)2 = 4 : 1
9. In the given figure PQRS is a cyclic quadrilateral PQ and SR produced meet at T.
(i) Prove ∆ TPS ~ ∆ TRQ.
(ii) Find SP if TP= 18cm, RQ= 4cm and TR= 6cm.
(iii) Find area of quadrilateral PQRS if area of ∆ PTS = 27 cm2 [2016]
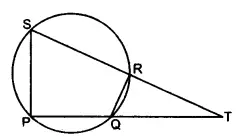
Solution: (ii) 12 cm (iii) 24 cm2
Step-by-step Explanation:
(i) In ΔTPS and △TRQ,
∠T is common.
∠TPS = ∠TRQ (exterior angle of a cyclic quadrilateral is equal to opposite interior angle)
∴ ΔTPS ~ ΔTRQ (A-A condition of similarity)
(ii) ∴ TP/TR = SP/RQ = TS/TQ
TP/TR = SP/RQ
18/6 = SP/4
SP = 12 cm
(iii) As ΔTPS ~ ΔTRQ, therefore
Area of ΔTPS / Area of ΔTRQ =(TP/TR)2 =(18/6)2 = 9/1
27/Area of ΔTRQ = 9/1
Area of ΔTRQ = 3 cm2
∴ area of quadrilateral PQRS = 27 – 3 = 24 cm2
10. ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC.
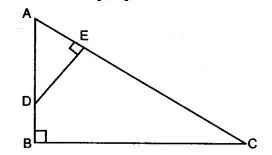
Prove that:
(i) ∆ADE ~ ∆ACB.
(ii) If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.
(iii) Find, area of ∆ ADE: area of quadrilateral BCED. [2015]
Solution: (ii) DE = 1 2/3 cm, AD = 4 1/3 cm (iii) 1 : 8
Step-by-step Explanation:
(i) In ΔADE and △ACB,
∠A is common.
∠AED = ∠ABC = 90° (given)
∴ ΔADE ~ ΔACB (A-A condition of similarity)
(ii) ∴ AD/AC = DE/BC = AE/AB
In right-angled ΔACB, by pythagoras theorem,
AC2 = AB2 + BC2
132 = AB2 + 52
AB = √169 – 25 = √144 = 12 cm
Now, AD/AC = AE/AB
AD/13 = 4/12
AD = 13/3 = 4 1/3 cm
DE/BC = AE/AB
DE/5 = 4/12
DE = 5/3 = 1 2/3 cm
(iii) As ΔADE ~ ΔACB, therefore
Area of ΔADE / Area of ΔACB =(AE/AB)2 =(4/12)2 = 1 : 9
∴ Area of ΔADE / Area of quadrilateral BCED = Area of ΔADE / Area of ΔABC – area of ΔADE
= 1/9-1= 1/8= 1 : 8
11. In ∆ABC, ∠ABC = ∠DAC, AB = 8 cm, AC = 4 cm, AD = 5 cm.
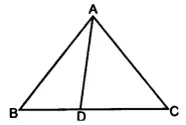
(i) Prove that ∆ACD is similar to ∆BCA.
(ii) Find BC and CD
(iii) Find area of ∆ACD : area of ∆ABC.
Solution: (ii) BC = 6.4 cm, CD = 2.5 cm (iii) 25 : 64
Step-by-step Explanation:
(i) In ΔACD and △BCA,
∠C is common.
∠DAC = ∠ABC (given)
∴ ΔACD ~ ΔBCA (A-A condition of similarity)
(ii) ∴ AC/BC = CD/AC = AD/AB
CD/AC = AD/AB
CD/4 = 5/8
CD = 5/2 = 2.5 cm
AC/BC = AD/AB
4/BC = 5/8
BC = 32/5 = 6.4 cm
(iii) Area of ΔACD / Area of ΔABC =(AD/AB)2 =(5/8)2 = 25 : 64
12. In the given figure, AB and DE are perpendiculars to BC.
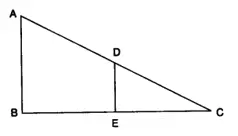
(i) Prove that ΔABC ~ ΔDEC
(ii) If AB = 6 cm, DE = 4 cm and AC = 15 cm. Calculate CD.
(iii) Find the ratio of the area of ΔABC : area of ΔDEC
Solution: (ii) CD = 10 cm (iii) 9 : 4
Step-by-step Explanation:
(i) In ΔABC and △DEC,
∠C is common.
∠ABC = ∠DEC = 90° (given)
∴ ΔABC ~ ΔDEC (A-A condition of similarity)
(ii) ∴ AB/DE = BC/EC = AC/CD
AB/DE = AC/CD
6/4 = 15/CD
CD = 10 cm
(iii) Area of ΔABC / Area of ΔDEC =(AB/DE)2 =(6/4)2 = 9 : 4
13. In the given figure Δ ABC and Δ AMP are right angled at B and M respectively.
Given, AB = 10 cm, AP = 15 cm and PM = 12 cm
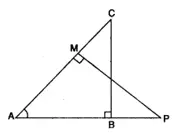
(i) Prove that Δ ABC ~ Δ AMP
(ii) Find AC and BC. [2012]
Solution: (ii) AC= 16 2/3 cm BC = 13 1/3 cm
Step-by-step Explanation:
(i) In ΔABC and △AMP,
∠A is common.
∠ABC = ∠AMP = 90° (given)
∴ ΔABC ~ ΔAMP (A-A condition of similarity)
(ii) In right-angled △AMP, by pythagoras theorem,
AP2 = AM2 + PM2
152 = AM2 + 122
AM = √225 – 144 = √81 = 9 cm
now, as ΔABC ~ ΔAMP
∴ AB/AM = BC/PM = AC/AP
AB/AM = BC/PM
10/9 = BC/12
BC =40/3 = 13 1/3 cm
AB/AM = AC/AP
10/9 = AC/15
AC = 50/3 = 16 2/3 cm
14. In the adjoining figure ABC is a right-angled triangle with ∠BAC = 90°,
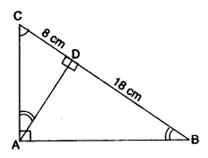
(i) Prove Δ ADB ~ Δ CDA
(ii) If BD = 18 cm and CD = 8 cm, find AD.
(iii) Find the ratio of area of Δ ADB is to area of Δ CDA. [2011]
Solution: (ii) AD = 12 cm (iii) 9 : 4
Step-by-step Explanation:
(i) In ΔADB, ∠ABD = 180°-(∠ADB + ∠DAB) = 90°– ∠DAB
In ΔCDA, ∠CAD = 90°– ∠DAB
Hence, ∠CAD = ∠ABD
In ΔADB and △CDA,
∠ADB = ∠CDA = 90° (given)
∠CAD = ∠ABD (proved above)
∴ ΔADB ~ ΔCDA (A-A condition of similarity)
(ii) ∴ AD/CD = BD/AD = AB/AC
AD/CD = BD/AD
AD/8 =18/AD
AD2 =18×8
AD = √144 = 12 cm
(iii) Area of ΔADB / Area of ΔCDA =(AD/CD)2 =(12/8)2 = 9 : 4
15. In the figure ABC is a triangle with ∠EDB = ∠ACB.
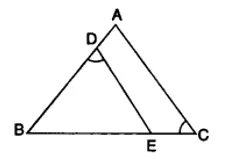
Prove that Δ ABC ~ Δ EBD
If BE = 6 cm, EC = 4 cm BD = 5 cm and area of ΔBED = 9 cm2 ,
Calculate the (i) length of AB
(ii) area of Δ ABC [2010]
Solution: (i) 12 cm (ii) 36 cm2
Step-by-step Explanation:
In ΔABC and △EBD,
∠B is common.
∠ACB = ∠BDE (given)
∴ ΔABC ~ ΔEBD (A-A condition of similarity)
∴ AB/BE = BC/BD = AC/ED
(i) so, AB/BE = BC/BD
AB/6 = 6+4/5
AB/6 = 10/5
AB = 12 cm
(iii) Area of ΔABC / Area of ΔEBD =(AB/BE)2 =(12/6)2
Area of ΔABC / 9 = 4/1
Hence, Area of ΔABC = 36 cm2
Subscribe my channel for more such educational content.
ICSE Related Links
Chapter-wise Quiz/MCQ/Test:
ICSE Chapter wise Quiz For Class 6
ICSE Chapter wise Quiz For Class 7
ICSE Chapter wise Quiz For Class 8
ICSE Chapter wise Quiz For Class 9
ICSE Chapter wise Quiz For Class 10
Sample Papers
Board Papers
ICSE Class 9 Board Exam Papers
ICSE Class 10 Board Exam Papers
CBSE Related Links
Chapter wise Quiz/MCQ/Test
CBSE Chapter-wise Quiz for Class 6
CBSE Chapter-wise Quiz for Class 7
CBSE Chapter-wise Quiz for Class 8
CBSE Chapter-wise Quiz for Class 9
CBSE Chapter-wise Quiz for Class 10

