ICSE Class 10 Maths Competency Focused Practice Questions Solution-Short Answer Questions 2

ICSE Class 10 Maths Competency Focused Practice Questions Solution

Short Answer Questions-2 (4 Marks Each)

Question 78
The following bill shows the GST rate and the marked price of items:

Grow Shree groceries

S.No.	Item	Marked price (₹)	Quantity	Rate of GST
1.	Wheat Flour (unpacked)	35.00	5 kg	x%
2.	Basmati Rice (Branded & packed)	180.00	5 kg	5%
3.	Surf Excel Quick Wash Detergent	220.00	y kg	18%

Find :

(a) the value of x if the total GST on wheat flour and basmati rice is ₹45.

(b) the value of y, if CGST paid for detergent powder is ₹39.60

Answer:

(a) Given, total GST on wheat flour and basmati rice is ₹45.

Total price of wheat flour = 35 × 5 = ₹175.

Total price of basmati rice = 180 × 5 = ₹900.

Given,

Total GST on wheat flour and basmati rice is ₹45.

∴ x% of ₹175 + 5% of ₹900 = ₹45

⇒1.75x + 45 = 45

⇒1.75x = 45 − 45

⇒1.75x=0

⇒x=0.

Hence, x = 0%.

(b) Total price of surf excel detergent = 220 × y = ₹220y.

GST on detergent powder = 18%

CGST = 18/2 = 9%

Given,

CGST paid for detergent powder is ₹39.60

∴9 % of ₹220y = ₹39.60

⇒9 × 2.20y=39.60

⇒ 2.20y = 39.60/9

⇒ 2.20y = 4.40

⇒ y =4.40/2.20 = 2.

Hence, y = 2 kg.

Total price = 35 × 5 = ₹175

GST = 0%

So, total price = ₹175.

For basmati rice,

Total price = 180 × 5 = ₹900

GST = 5%

So, total price = ₹900 + 5% of ₹900

= ₹900 + ₹45 = ₹945.

For detergent powder,

Total price = 220 × 2 = ₹440

GST = 18%

So, total price = ₹440 + 18% of ₹440

= ₹440 + ₹79.20 = ₹519.20

Total bill = ₹(175 + 945 + 519.20) = ₹1639.20

Hence, total bill = ₹1639.20

Question 79
Amit deposited ₹600 per month in a recurring deposit account. The bank pays a simple interest of 12% p.a. Calculate the:

(a) number of monthly installments Amit deposits to get a maturity amount of ₹11826?

(b) total interest paid by the bank.

Answer:

(a) Let money be deposited for n months.

By formula,

\[M.V.=Pn+\left(P\times\frac{n(n+1)}{2\times12}\times\frac r{100}\right)\\\Rightarrow11826=600n+\left(600\times\frac{n(n+1)}{2\times12}\times\frac{12}{100}\right)\\\Rightarrow11826=600n+3n(n+1)\\\Rightarrow3n^2+3n+600n-11826=0\\\Rightarrow3n^2+603n-11826=0\\\Rightarrow n^2+201n-3942=0\\\Rightarrow n^2+219n-18n-3942=0\\\Rightarrow n(n+219)-18(n+219)=0\\\Rightarrow(n+219)(n-18)=0\\Either\;(n+219)=0\;or\;(n-18)=0\\\Rightarrow\;n=-219\;or\;18\\\\\]

Since, no. of months cannot be negative.

∴ n = 18.

Hence, number of monthly installments = 18.

(b) By formula,

Total Interest = M.V. – Pn

= 11826 – (600 x 18)

= 11826 – 10800

= 1026.

Hence, total interest paid = ₹1026.

= ₹600 × 18

= ₹10800.

Hence, total amount deposited by Amit = ₹10800.

Question 80
Aman has 500, ₹100 shares of a company quoted at ₹120, paying a 10% dividend. When the share price rises to ₹200 each, he sells all his shares. He invests half of the sale proceeds in ₹10, 12% shares at ₹25, and the remaining sale proceeds in ₹400, 9% shares at ₹500.

Find his:

(a) sales proceeds.

(b) investment in ₹10, 12% shares at ₹25.

(d) change in income.

Answer:

(a) No. of shares sold by Aman = 500

M.V. while selling = ₹200.

Sale proceeds = 500 × ₹200 = ₹1,00,000

Hence, sale proceeds = ₹1,00,000.

(b) Given,

Aman invests half of the sale proceeds in ₹10, 12% shares at ₹25.

∴ Investment = Sale proceeds/2 = 100000/2

= ₹50,000.

Hence, investment in ₹10, 12% shares at ₹ 25 = ₹50,000.

\[Income=\frac{n\times r\times f}{100}\\I=\frac{500\times10\times100}{100}\\I=5000\\\]

Hence, original income = ₹5,000.

(d) Aman invests ₹50,000 in each of the new shares.

For 1st share:

N.V. = ₹10

Dividend = 12%

M.V. = ₹25

No. of shares bought = 50000/25

= 2000.

\[Income=\frac{n\times r\times f}{100}\\I=\frac{2000\times12\times10}{100}\\I=2400\]

= ₹2400.

For 2nd share :

N.V. = ₹400

Dividend = 9%

M.V. = ₹500

No. of shares bought = 50000/500

= 100

\[Income=\frac{n\times r\times f}{100}\\I=\frac{100\times9\times400}{100}\\I=3600\]

= ₹ 3,600.

New income = ₹3,600 + ₹2,400 = ₹6,000

Change in income = New income – Original income = ₹(6,000 – 5,000) = ₹1,000.

Hence, change in income = ₹1,000 (gain).

Question 81
Solve the following inequation.

\[\frac{11+3x}5\geq3-x>-\frac32,x\in R\]

(a) Write the solution set.

(b) Represent the solution on the number line.

Answer:

(a)

\[Solving,\;\frac{11+3x}5\geq3-x\\\Rightarrow11+3x\geq15-5x\\\Rightarrow3x+5x\geq15-11\\\Rightarrow8x\geq4\\\Rightarrow x\geq\frac12\\Solving,\;3-x>-\frac32\\\Rightarrow6-2x>-3\\\Rightarrow-2x>-3-6\\\Rightarrow-2x>-9\\\Rightarrow2x<9\\\Rightarrow x<\frac92\\\therefore Solution\;set=\left\{x:\frac12\leq x<\frac92,x\in R\right\}\]

(b)

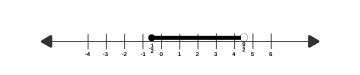
Question 82
Determine whether the following quadratic equation has real roots.

5𝑥² − 9𝑥 + 4 = 0

(a) Give reasons for your answer.

(b) If the equation has real roots, identify them.

Answer:

(a) Given, equation : 5𝑥² − 9𝑥 + 4 = 0

Comparing above equation with ax² + bx + c = 0, we get:

a = 5, b = -9 and c = 4.

Discriminant (D) = b² – 4ac = (-9)² – 4 × 5 × 4 = 81 – 80 = 1.

Since, D > 0,

Hence, equation 5𝑥² − 9𝑥 + 4 = 0 has real roots.

(b) Solving,

⇒ 5𝑥² − 9𝑥 + 4 = 0

⇒ 5𝑥² – 5x – 4x + 4 = 0

⇒ 5x(x – 1) – 4(x – 1) = 0

⇒ (5x – 4)(x – 1) = 0

⇒ Either 5x – 4 = 0 or x – 1 = 0

⇒ 5x = 4 or x = 1

⇒ x = 4/5 or x = 1.

Hence, roots of the equation are 4/5 and 1.

Question 83
The profit in rupees in a local restaurant and the number of customers who visited the restaurant are tabulated below for each week for one month.

Week number	Week 1	Week 2	Week 3	Week 4
Number of customers	1400	5600	x	3212
Profit in ₹	28000	112000	32140	y

Find :

(a) if the number of customers and profit per week in continued proportion or not? Justify your answer.

(b) the value of x and y.

Answer:

(a)

\[\frac{1400}{28000}=\frac{5600}{112000}=\frac1{20}\\So,\;the\;number\;of\;customers\;and\;profit\;per\;\\week\;are\;in\;proportion.\\But,\\\frac{1400}{28000}\neq\frac{28000}{5600}\neq\frac{5600}{112000}\\\therefore The\;no.\;of\;customers\;and\;profit\;per\;\\week\;are\;not\;in\;continued\;proportion.\]

Hence, number of customers and profit per week are in proportion but not in continued proportion.

(b) As, Number of customers and profit per week are in proportion.

\[\therefore\frac{1400}{28000}=\frac x{32140}\\\Rightarrow\frac1{20}=\frac x{32140}\\\Rightarrow20x=32140\\\Rightarrow x=\frac{32140}{20}\\\Rightarrow x=1607\\\\\frac{1400}{28000}=\frac{3212}y\\\Rightarrow\frac1{20}=\frac{3212}y\\\Rightarrow y=3212\times20\\\Rightarrow y=64240\]

Hence, x = 1607 and y = 64240.

Question 84
Given, 9𝑥² – 4 is a factor of 9𝑥³– m𝑥² – n𝑥 + 8:

(a) find the value of m and n using the remainder and factor theorem.

(b) factorise the given polynomial completely.

Answer

(a) Simplifying 9𝑥² – 4, we get :

⇒ 9𝑥² – 4

⇒ (3𝑥)² – 2²

⇒ (3𝑥 + 2)(3𝑥 – 2).

We know that,

If (x – a) is a factor of f(x), then f(a) = 0.

Given,

9𝑥² – 4 is a factor of 9𝑥³ – m𝑥² – n𝑥 + 8.

∴ (3𝑥 + 2) and (3𝑥 – 2) are the factors of 9𝑥³ – m𝑥² – n𝑥 + 8.

⇒ 3𝑥 + 2 = 0

⇒ 3𝑥 = -2

⇒ 𝑥 = -2/3

Substituting x = -2/3 in 9𝑥³ – m𝑥² – n𝑥 + 8, we get remainder = 0.

\[9\left(\frac{-2}3\right)^3\;-\;m\left(\frac{-2}3\right)^2\;-\;n\left(\frac{-2}3\right)+\;8\;=\;0\\\Rightarrow9\times\frac{-8}{27}-m\times\frac49+\frac{2n}3+8=0\\\Rightarrow\frac{-8}3-\frac{4m}9+\frac{2n}3+8=0\\\Rightarrow\frac{-24-4m+6n+72}9=0\\\Rightarrow48-4m+6n=0\\\Rightarrow24-2m+3n=0\\\Rightarrow2m-3n=24\;……\;(1)\]

Now, (3𝑥 – 2) is also the factor of 9𝑥³ – m𝑥² – n𝑥 + 8.

⇒ 3𝑥 – 2 = 0

⇒ 𝑥 = 2/3

Substituting x = 2/3 in 9𝑥³ – m𝑥² – n𝑥 + 8, we get remainder = 0.

\[9\left(\frac23\right)^3\;-\;m\left(\frac23\right)^2\;-\;n\left(\frac23\right)+\;8\;=\;0\\\Rightarrow9\times\frac8{27}-m\times\frac49-\frac{2n}3+8=0\\\Rightarrow\frac83-\frac{4m}9-\frac{2n}3+8=0\\\Rightarrow\frac{24-4m-6n+72}9=0\\\Rightarrow96-4m-6n=0\\\Rightarrow48-2m-3n=0\\\Rightarrow2m+3n=48\;……\;(2)\]

Adding equations (1) and (2), we get :

⇒ 3n – 2m + 2m + 3n = -24 + 48

⇒ 6n = 24

⇒ n = 4

Substituting value of n in equation (1), we get :

⇒ 3(4) – 2m = -24

⇒ 12 – 2m = -24

⇒ -2m = -24 – 12

⇒ -2m = -36

⇒ m = 18

Hence, m = 18 and n = 4.

(b) Substituting value of m and n in 9𝑥³ – m𝑥² – n𝑥 + 8, we get :

9𝑥³ – 18𝑥² – 4𝑥 + 8

Dividing 9𝑥³ – 18𝑥² – 4𝑥 + 8 by 9𝑥² – 4, we get :

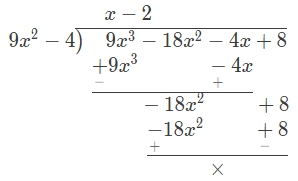
∴ 9𝑥³ – 18𝑥² – 4𝑥 + 8 = (9𝑥² – 4)(𝑥 – 2)

= (3𝑥 + 2)(3𝑥 – 2)(𝑥 – 2).

Hence, factors are (3𝑥 + 2), (3𝑥 – 2) and (𝑥 – 2).

Question 85
The marks scored by 100 students are given below:

Marks scored	No. of students
0 – 10	4
10 – 20	5
20 – 30	9
30 – 40	7
40 – 50	13
50 – 60	12
60 – 70	15
70 – 80	11
80 – 90	14
90 – 100	10

A student in the class is selected at random. Find the probability that the student has scored

(a) less than 20

(b) below 60 but 30 or more

(d) above 89.

Answer:

Marks scored	No. of students (f)	Cumulative frequency (cu. f)
0 – 10	4	4
10 – 20	5	9
20 – 30	9	18
30 – 40	7	25
40 – 50	13	38
50 – 60	12	50
60 – 70	15	65
70 – 80	11	76
80 – 90	14	90
90 – 100	10	100

(a) By formula,

Probability that student has scored less than 20

\[=\frac{No.\;of\;students\;who\;scored\;less\;than\;20}{Total\;no.\;of\;students}\\=\frac9{100}\]

(b) No. of students who scored less than 60 = 50

No. of students who scored less than 30 = 18

∴ No. of students who score below 60 but 30 or more = 50 – 18 = 32.

Probability that student has scored below 60 but 30 or more:

\[=\frac{No.\;of\;students\;scoring\;between\;60\;and\;30}{Total\;no.\;of\;students}\\=\frac{32}{100}=\frac8{25}\]

No. of students who scored less than 70 = 65

Total no. of students = 100

∴ No. of students who score more than or equal to 70 = 100 – 65 = 35.

Probability that student has scored more than or equal to 70:

\[=\frac{No.\;of\;students\;scoring\;more\;than\;or\;equal\;to\;70}{Total\;no.\;of\;students}\\=\frac{35}{100}=\frac7{20}\]

(d) No. of students those who have scored more than 89 = No. of students who has scored between 90 -100 = 10.

Probability that student has scored more than 89:

\[=\frac{No.\;of\;students\;scoring\;more\;than\;89}{Total\;no.\;of\;students}\\=\frac{10}{100}=\frac1{10}\]

Question 86

\[Given\;matrix\;A=\begin{bmatrix}x&1\\y&2\end{bmatrix}\;and\;B=\begin{bmatrix}x\\x-2\end{bmatrix}\;\\such\;that\;AB\;is\;a\;null\;matrix.\;Find:\\(a)\;order\;of\;the\;null\;matrix.\\(b)\;possible\;values\;of\;x\;and\;y.\]

Answer:

Given,

AB is a null matrix.

Let AB = X, where X is a null matrix of order a × b.

⇒ AB = X

⇒ A_{2 × 2} × B_{2 × 1} = X_{a × b}

We know that,

The resultant matrix has no. of rows equal to the rows in the first matrix and no. of columns equal to the no. of columns in the second matrix.

∴ a = 2 and b = 1.

\[Given\;AB=X\\\begin{bmatrix}x&1\\y&2\end{bmatrix}\;\begin{bmatrix}x\\x-2\end{bmatrix}\;=\begin{bmatrix}0\\0\end{bmatrix}\\\begin{bmatrix}x^2+1(x-2)\\xy+2(x-2)\end{bmatrix}=\begin{bmatrix}0\\0\end{bmatrix}\\\begin{bmatrix}x^2+x-2\\xy+2x-4\end{bmatrix}=\begin{bmatrix}0\\0\end{bmatrix}\\\]

From equation (1) :

⇒ x² + x – 2 = 0

⇒ x² + 2x – x – 2 = 0

⇒ x(x + 2) – 1(x + 2) = 0

⇒ (x – 1)(x + 2) = 0

⇒ x – 1 = 0 or x + 2 = 0

⇒ x = 1 or x = -2.

From equation (2) :

⇒ xy + 2x – 4 = 0

Substituting x = 1, we get :

⇒ 1.y + 2.1 – 4 = 0

⇒ y + 2 – 4 = 0

⇒ y – 2 = 0

⇒ y = 2.

Substituting x = -2, we get :

⇒ (-2).y + 2.(-2) – 4 = 0

⇒ -2y – 4 – 4 = 0

⇒ -2y – 8 = 0

⇒ -2y = 8

⇒ y = -4

Hence, x = 1, y = 2 or x = -2, y = -4.

Question 87
The sum of a certain number of terms of the Arithmetic Progression (A.P.) 20, 17, 14, ……. is 65. Find the:

(a) number of terms.

(b) last term.

Answer:

(a) Let the no. of terms be n.

Here, first term (a) = 20

common difference (d) = 17 – 20 = -3

By formula,

\[S_{n\;}=\frac n2\left\{2a+(n-1)d\right\}\\\Rightarrow65=\frac n2\left\{2\times20+(n-1)(-3)\right\}\\\Rightarrow65=\frac n2\left\{40-3n+3\right\}\\\Rightarrow65=\frac n2(43-3n)\\\Rightarrow130=43n-3n^2\\\Rightarrow3n^2-43n+130=0\\\Rightarrow3n^2-30n-13n+130=0\\\Rightarrow3n(n-10)-13(n-10)=0\\\Rightarrow(n-10)(3n-13)=0\\Either\;(n-10)=0\;or\;(3n-13)=0\\n\;=\;10\;or\;\frac{13}3\]

Since, no. of terms cannot be in fraction.

∴ n = 10.

Hence, no. of terms = 10.

(b) By formula,

Last term (l) = a + (n – 1)d

= 20 + (10 – 1) × (-3)

= 20 + 9 × (-3)

= 20 – 27

= -7.

Hence, last term = -7.

Question 88
(a) Point P(2, -3) on reflection becomes P'(2, 3). Name the line of reflection (say L₁).

(b) Point P’ is reflected to P” along the line (𝐿₂), which is perpendicular to the line 𝐿₁ and passes through the point, which is invariant along both axes. Write the coordinates of P”.

(d) Point P is reflected to P”’ on reflection through the point named in the answer of part I of this question. Write the coordinates of P”’. Comment on the location of the points P” and P”’.

Answer

(a) P(2, -3) ⇒ P'(2, 3)

Since, sign of y-coordinate changes.

∴ L₁ = x-axis

Hence, point P becomes P’ on reflection in x-axis.

(b) Origin remains invariant on reflection along both the axes.

L₂ is perpendicular to L₁.

It means L₂ is perpendicular to x-axis and passes through (0, 0).

∴ L₂ is y-axis.

P'(2, 3) on reflection in y-axis becomes P”(-2, 3).

Hence, coordinates of P” = (-2, 3).

Hence, coordinates of intersection of lines L₁ and L₂ is (0, 0).

(d) P(2, -3) on reflection in origin becomes P”'(-2, 3).

Since, P” and P”’ have similar co-ordinates.

Hence, P” and P”’ are coincident points.

Question 89
In the given figure, if the line segment AB is intercepted by the y-axis and x-axis at C and D, respectively, such that AC : AD = 1 : 4 and D is the midpoint of CB. Find the coordinates of D, C and B.

In the given figure, if the line segment AB is intercepted by the y-axis and x-axis at C and D, respectively, such that AC : AD = 1 : 4 and D is the midpoint of CB. Find the coordinates of D, C and B.

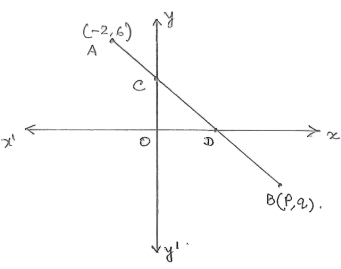
maths-competency-focused-practice-questions-solution

Answer:

Let coordinates of C be (0, y) and D be (x, 0).

Given,

AC : AD = 1 : 4

Let AC = a and AD = 4a.

From figure,

⇒ AD = AC + CD

⇒ 4a = a + CD

⇒ CD = 4a – a = 3a

AC : CD = 1 : 3.

By section formula,

\[(x\;,\;y)=\left(\frac{mx_2+nx_1}{m+n},\frac{my_2+ny_1}{m+n}\right)\\\Rightarrow x=\frac{mx_2+nx_1}{m+n}\\\Rightarrow0=\frac{1\times x+3\times(-2)}{1+3}\\\Rightarrow0=\frac{x-6}4\\\Rightarrow x-6=0\\\Rightarrow x=6\\\]

∴ Co ordinates of D = (6 , 0)

\[Now,\;y=\frac{my_2+ny_1}{m+n}\\\Rightarrow y=\frac{1\times0+3\times6}{1+3}\\\Rightarrow y=\frac{18}4\\\Rightarrow y=\frac92\\Hence,\;coordinates\;of\;C=(0,\frac92)\\\]

Given, D is the mid-point of CB.

\[\therefore\;coordinates\;of\;D=\left(\frac{x_1+x_2}2,\frac{y_1+y_2}2\right)\\(6,0)=\left(\frac{0+p}2,\frac{{\displaystyle\frac92}+q}2\right)\\6=\frac{0+p}2\;and\;0=\frac{\displaystyle\frac92+q}2\\p=12\;and\;q=-\frac92\\Hence\;coordiantes\;of\;B=(12,-\frac92).\]

Question 90
Find the equation of the straight line perpendicular to the line x + 2y = 4, which cuts an intercept of 2 units from the positive y-axis. Hence, find the intersection point of the two lines.

Answer:

Given,

Equation: x + 2y = 4

⇒ 2y = -x + 4

⇒ y =-x/2 + 4/2

⇒ y =-x/2 + 2

Comparing the above equation with y = mx + c we get :

⇒ m = -1/2 and c = 2

Let slope of line perpendicular to line x + 2y = 4 be m₁ (-1/2).

We know that,

Product of slope of perpendicular lines = -1.

⇒ m₁ x m₂ = -1

⇒ -1/2 x m₂ = -1

⇒ m₂ = 2

Substituting values we get :

⇒ y = mx + c

⇒ y = 2x + 2.

Simultaneously solving equation :

⇒ x + 2y = 4 ………(1)

⇒ y = 2x + 2 …….(2)

Substituting value of y from equation (2) in (1), we get :

⇒ x + 2(2x + 2) = 4

⇒ x + 4x + 4 = 4

⇒ 5x = 4 – 4

⇒ 5x = 0

⇒ x = 0.

Substituting value of x in equation (2), we get :

⇒ y = 2(0) + 2 = 2.

Hence, equation of required line is y = 2x + 2 and point of intersection = (0, 2).

Question 91
While preparing a PowerPoint presentation, ∆ ABC is enlarged along the side BC to ∆ AB’C’, as shown in the diagram, such that BC ∶ B’C’ is 3 ∶ 5. Find:

(a) AB ∶ BB’

(b) length AB, if BB’ = 4 cm.

(d) ar (∆ ABC) : ar (quad. BB’C’C).

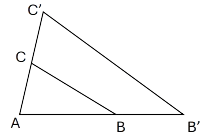
Answer:

Since, ∆ ABC is enlarged along the side BC to ∆ AB’C’.

∴ ∆ ABC and ∆ AB’C’ are similar triangles.

(a) We know that,

Ratio of corresponding sides of similar triangles are proportional.

\[\therefore\;\frac{AB}{AB’}=\frac{BC}{B’C’}=\frac35\\\Rightarrow\frac{AB}{BB’}=\frac{AB}{AB’-BB’}\\\;\;\;\;\;\;\;\;\;\;\;\;\;=\frac3{5-3}=\frac32\]

Hence, AB : BB’ = 3 : 2.

(b)

\[As,\frac{AB}{BB’}=\frac32\\\therefore\frac{AB}4=\frac32\\\Rightarrow AB=\frac{12}2=6\]

Hence, AB = 6 cm.

∴ BC || B’C’

In ∆ ABC and ∆ AB’C’,

⇒ ∠BAC = ∠B’AC’ (Common angle)

⇒ ∠ABC = ∠AB’C’ (Corresponding angle are equal)

∴ ∆ ABC ~ ∆ AB’C’ (By A.A. axiom).

Hence, proved that ∆ ABC ~ ∆ AB’C’.

(d) We know that,

The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.

\[\frac{ar.\;\bigtriangleup ABC}{ar.\;\bigtriangleup AB’C’}=\left(\frac{BC}{B’C’}\right)^2\\\Rightarrow\frac{ar.\;\bigtriangleup ABC}{ar.\;\bigtriangleup AB’C’}=\left(\frac35\right)^2=\frac9{25}\\\therefore\frac{ar.\;\bigtriangleup ABC}{ar.\;quad.\;BB’C’C}=\frac{ar.\;\bigtriangleup ABC}{ar.\;(\bigtriangleup AB’C’-\bigtriangleup ABC)}\\\Rightarrow\frac{ar.\;\bigtriangleup ABC}{ar.\;quad.\;BB’C’C}=\frac9{25-9}\\\Rightarrow\frac{ar.\;\bigtriangleup ABC}{ar.\;quad.\;BB’C’C}=\frac9{16}\]

Hence, area of ∆ ABC : area of quadrilateral BB’C’C = 9 : 16.

Question 92
The approximate volume of a human eye is 6.5 cm³. The volume of a laboratory model (excluding base and stand) of the human eye is 1404 cm³.

(a) State whether the scale factor k is less than, equals to or greater than 1.

(b) Calculate the:

(i) value of k

(ii) diameter of the human eye if the radius of the model is 7.2 cm.

(iii) the external surface area of the human eye if the surface area of the model is 651.6 cm².

Answer:

(a) Scale factor is greater than 1 as volume of model is greater than the original eye.

(b)

(i) By formula,

Volume of a model eye = k³ x volume of human eye

⇒ 6.5 = k³ x 1404

⇒ k³ = 6.5/1404

⇒ k³ = 1/216

⇒ k=∛1/216

⇒ k= 1/6 = 1 : 6

Hence, scale factor (k) = 6.

(ii) By formula,

Radius of model eye = k x Radius of human eye

⇒ Radius of human eye = 7.2/6 = 1.2 cm

Diameter of human eye = 1.2 × 2 = 2.4 cm

Hence, diameter of human eye = 2.4 cm.

(iii) By formula,

Surface area of the model eye = k² x surface area of the human eye

⇒ 651.6 = 6² x surface area of the human eye

⇒ surface area of the human eye = 651.6/36 = 18.1 cm²

Hence, surface area of human eye = 18.1 cm².

Question 93
In the adjoining diagram PQ, PR and ST are the tangents to the circle with centre O and radius 7 cm. Given OP = 25 cm. Find :

(a) length of ST

(b) value of ∠OPQ, i.e. θ

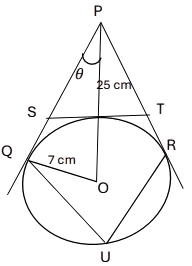
Answer:

(a) We know that,

The radius of a circle and tangent are perpendicular at the point of contact.

∴ ∠PQO = 90°

⇒ PO² = PQ² + OQ²

⇒ 25² = PQ² + 7²

⇒ 625 = PQ² + 49

⇒ PQ² = 625 – 49

⇒ PQ² = 576

⇒ PQ = 24 cm.

In △ POQ,

\[\tan\theta=\frac pb=\frac{OQ}{PQ}\\\Rightarrow t\mathrm{an}\theta=\frac7{24}\;……\;(1)\]

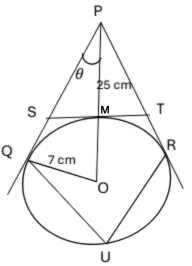
From figure,

⇒ ∠PMS = 90°

⇒ PM = OP – OM = 25 – 7 = 18 cm.

\[\tan\theta=\frac pb=\frac{SM}{PM}\\\Rightarrow\frac7{24}=\frac{SM}{18}\\\Rightarrow SM=\frac{7\times18}{24}\;\\\Rightarrow SM=\frac{21}4\\\Rightarrow ST=2\times SM\\=2\times\frac{21}4=\frac{21}2=10.5\;cm\]

Hence, ST = 10.5 cm.

(b) From equation (1),

⇒ tan θ = 7/24

⇒ tan θ = 0.292

⇒ tan θ = tan 16° 16′ (from trigonometric table)

⇒ θ = 16° 16′.

Hence, θ = 16° 16′.

⇒ ∠POQ + ∠PQO + ∠QPO = 180°

⇒ ∠POQ + 90° + 16° 16′ = 180°

⇒ ∠POQ + 106° 16′ = 180°

⇒ ∠POQ = 180° – 106° 16′ = 73° 44′ = 74°.

We know that,

Tangent from an external point to the circle are equal in length.

∴ PQ = PR.

Also,

OR = OQ (Both equal to radius of circle)

In △ POQ and △ POR,

⇒ PQ = PR (Proved above)

⇒ OQ = OR (Radius of same circle)

⇒ PO = PO (Common side)

∴ △ POQ ≅ △ POR (By S.S.S. axiom)

We know that,

Corresponding parts of congruent triangles are equal.

∴ ∠POR = ∠POQ = 74°

From figure,

⇒ ∠QOR = ∠POR + ∠POQ = 74° + 74° = 148°.

We know that,

The angle subtended by an arc of a circle at its center is twice the angle it subtends anywhere on the circle’s circumference.

⇒ ∠QOR = 2∠QUR

⇒ ∠QUR = 148/2 = 74°

Hence, ∠QUR = 74°.

Question 94
Use ruler and compass to answer this question. Construct a triangle ABC where AB = 5.5 cm, BC = 4.5 cm and angle ABC = 135°. Construct the circumcircle to the triangle ABC. Measure and write down the length of AC.

Answer:

Steps of construction :

Draw a line segment BC = 4.5 cm

Construct XB such that ∠XBC = 135°.

Cut AB = 5.5 cm from XB.

Join and measure AC.

Draw the perpendicular bisectors of BC and AB.

Mark point O the intersection of the perpendicular bisectors.

With O as center and radius as OA, draw a circle touching the vertices A, B and C.

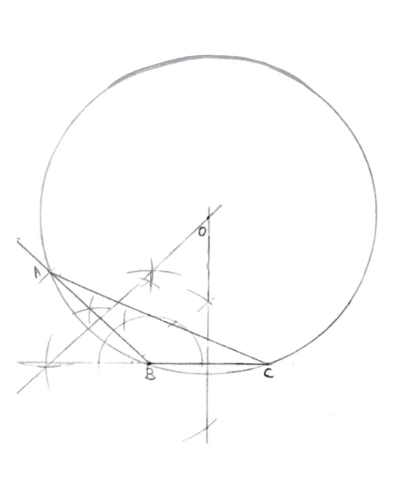
maths-competency-focused-practice-questions-solution-construction

On measuring AC = 9.1 cm and radius = 6.5 cm.

Question 95
The curved surface area of a right circular cone is half of another right circular cone. If the ratio of their slant heights is 2 : 1 and that of their volumes is 3 : 1, find ratio of their:

(a) radii

(b) heights

Answer:

(a) Let radius of smaller and larger cone be r and R, respectively.

Let height of smaller and larger cone be h and H, respectively.

Let slant height of smaller and larger cone be l and L respectively.

Ratio of their slant heights is 2 : 1.

∴ l : L = 2 : 1.

let l be 2x and L be x

Curved surface area of a right circular cone is half of the other right circular cone.

∴ πrl = 1/2 πRL

⇒ rl = 1/2 RL

⇒ r x 2x = 1/2 x R x x

⇒ r : R = 1 : 4

Hence, ratio of the radii = 1 : 4.

(b) Let volume of cone with smaller curved surface area be v and that with larger curved surface area be V.

Volumes are in the ratio 3 : 1.

∴ v : V = 3 : 1

\[\frac{Volume\;of\;smaller\;CSA\;cone}{Volume\;of\;larger\;CSA\;cone}=\frac31\\\frac{\displaystyle\frac1{3\mathrm{πr}^2\mathrm h}}{\displaystyle\frac1{3\mathrm{πR}^2\mathrm H}}=\frac31\\\frac{\displaystyle r^2\mathrm h}{\displaystyle R^2\mathrm H}=\frac31\\\frac{\displaystyle1^2\mathrm h}{\displaystyle4^2\mathrm H}=\frac31\\\frac{\displaystyle\mathrm h}{\displaystyle16\mathrm H}=\frac31\\\frac{\displaystyle\mathrm h}{\displaystyle\mathrm H}=\frac{48}1\\\therefore h:H=48:1\\\\\]

Hence, ratio of heights = 48 : 1.

Question 96
A cylindrical drum is unloaded from a truck by rolling it down along a wooden plank. The length of the plank is 10 m and it is making an angle of 10° with the horizontal ground. Find the height from which the cylindrical drum was rolled down. Give your answer correct to 3 significant figures.

Answer:

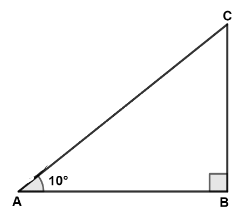
According to the above figure,

\[\sin\;\theta=\frac ph=\frac{BC}{AB}\\\sin\;10^\circ=\frac{BC}{10}\\0.1736=\frac{\mathrm{BC}}{10}\\BC=1.736\;\sim1.74\;m\\\]

Hence, height from which the cylindrical drum was rolled down = 1.74 m.

Question 97
The data given below shows the marks of 12 students in a test, arranged in ascending order :

2, 3, 3, 3, 4, x, x + 2, 8, p, q, 8, 9.

If the given value of the median and mode is 6 and 8 respectively, then find the values of x, p, q.

Answer:

\[Median=\frac{{\displaystyle\frac n2}th\;term+({\displaystyle\frac n2}+1)th\;term}2\\\Rightarrow6=\frac{\displaystyle\frac{12}2th\;term+(\frac{12}2+1)th\;term}2\\\Rightarrow6=\frac{\displaystyle6th\;term+7th\;term}2\\\Rightarrow6=\frac{\displaystyle x+x+2}2\\\Rightarrow2x+2=12\\\Rightarrow2x=10\\\Rightarrow x=5\]

Numbers :

2, 3, 3, 3, 4, 5, 7, 8, p, q, 8, 9.

Since, mode = 8, it means 8 occurs for the most times in the series.

Since, 3 occurs 3 times in the series,

∴ 8 must occur for atleast 4 times in order to be the mode.

∴ p = q = 8.

Hence, x = 5, p = 8 and q = 8.

Question 98
Solve the linear inequation, write down the solution set and represent it on the real number line :

5(2 – 4x) > 18 – 16x > 22 – 20x, x ∈ R

Answer

Solving 5(2 – 4x) > 18 – 16x

⇒ 10 – 20x > 18 – 16x

⇒ -16x + 20x < 10 – 18

⇒ 4x < -8

⇒ x < -2

Solving 18 – 16x > 22 – 20x

⇒ 20x – 16x > 22 – 18

⇒ 4x > 4

⇒ x > 1

Solution set: {x : x < -2 or x > 1, x ∈ R}

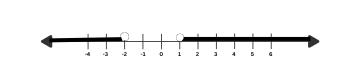
Hence, solution set = {x : x < -2 or x > 1, x ∈ R}.

Question 99
If a polynomial x³ + 2x² – ax + b leaves a remainder -6 when divided by x + 1 and the same polynomial has x – 2 as a factor, then find the values of a and b.

Answer:

Given,

x³ + 2x² – ax + b leaves a remainder -6 when divided by x + 1.

⇒ x + 1 = 0

⇒ x = -1.

Let f(x) = x³ + 2x² – ax + b, then f(-1) = -6.

⇒ f(-1) = -6

⇒ (-1)³ + 2(-1)² – a(-1) + b = -6

⇒ -1 + 2(1) + a + b = -6

⇒ -1 + 2 + a + b = -6

⇒ a + b + 1 = -6

⇒ a + b = -6 – 1

⇒ a + b = -7 ……..(1)

Given ,

x – 2 is a factor of f(x).

⇒ x – 2 = 0

⇒ x = 2.

f(2) = 0

⇒ 2³ + 2(2)² – 2a + b = 0

⇒ 8 + 2(4) – 2a + b = 0

⇒ 8 + 8 – 2a + b = 0

⇒ 16 – 2a + b = 0

⇒ 2a – b = 16 ……(2)

Adding equation (1) and (2), we get :

⇒ a + b + 2a – b = -7 + 16

⇒ 3a = 9

⇒ a = 3.

Substituting value of a = 3 in equation (1), we get :

⇒ 3 + b = -7

⇒ b = -7 – 3 = -10.

Hence, a = 3 and b = -10.

Question 100

\[If\;A=\begin{bmatrix}-1&3\\2&0\end{bmatrix},\;B=\begin{bmatrix}1&-2\\0&3\end{bmatrix},\;C=\begin{bmatrix}1&-4\end{bmatrix}\;and\;D=\begin{bmatrix}4\\1\end{bmatrix}.\]

(a) Is the product AC possible? Justify your answer.

(b) Find the matrix X, such that X = AB + B² − DC

Answer:

(a) Order of matrix A = 2 × 2, Order of matrix C = 1 × 2

As the no. of columns in A is not equal to the no. of rows in C,

Hence, product AC is not possible.

(b)

\[AB=\;\begin{bmatrix}-1&3\\2&0\end{bmatrix}\begin{bmatrix}1&-2\\0&3\end{bmatrix}\\=\begin{bmatrix}(-1)\times1+3\times0&(-1)(-2)+3\times3\\2\times1+0\times0&2(-2)+0\times3\end{bmatrix}\\=\begin{bmatrix}-1&11\\2&-4\end{bmatrix}\\B^2=\begin{bmatrix}1&-2\\0&3\end{bmatrix}\begin{bmatrix}1&-2\\0&3\end{bmatrix}\\=\begin{bmatrix}1\times1+(-2)\times0&1\times(-2)+(-2)\times3\\0\times1+3\times0&0\times(-2)+3\times3\end{bmatrix}\\=\begin{bmatrix}1&-8\\0&9\end{bmatrix}\\DC=\begin{bmatrix}4\\1\end{bmatrix}\begin{bmatrix}1&-4\end{bmatrix}\\=\begin{bmatrix}4\times1&4\times(-4)\\1\times1&1\times(-4)\end{bmatrix}\\=\begin{bmatrix}4&-16\\1&-4\end{bmatrix}\\X\;=\;AB\;+\;B^2\;-\;DC\\=\begin{bmatrix}-1&11\\2&-4\end{bmatrix}+\begin{bmatrix}1&-8\\0&9\end{bmatrix}-\begin{bmatrix}4&-16\\1&-4\end{bmatrix}\\=\begin{bmatrix}-1+1-4&11-8+16\\2+0-1&-4+9+4\end{bmatrix}\\=\begin{bmatrix}-4&19\\1&9\end{bmatrix}\\Hence,\;X=\begin{bmatrix}-4&19\\1&9\end{bmatrix}\]

Question 101
In the given figure (not drawn to scale), BC is parallel to EF, CD is parallel to FG, AE : EB = 2 : 3, ∠BAD = 70°, ∠ACB = 105°, ∠ADC = 40° and AC is bisector of ∠BAD.

(a) Prove Δ AEF ~ Δ AGF

(b) Find :

(i) AG : AD

(ii) area of Δ ACB: area Δ ACD

(iii) area of quadrilateral ABCD: area of Δ ACB.

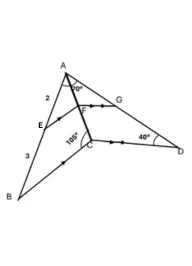
Answer:

(a) In Δ AEF,

⇒ ∠AFE = ∠ACB = 105° (Corresponding angle are equal)

⇒ ∠EAF =∠BAD/2

⇒70°/2 = 35° (AC is the bisector of ∠BAD)

By angle sum property of triangle,

⇒ ∠AFE + ∠EAF + ∠AEF = 180°

⇒ 105° + 35° + ∠AEF = 180°

⇒ 140° + ∠AEF = 180°

⇒ ∠AEF = 180° – 140° = 40°.

∠AGF = ∠ADC = 40° (Corresponding angles are equal)

In Δ AGF,

⇒ ∠GAF =∠BAD/2

⇒ 70°/2 = 35° (AC is the bisector of ∠BAD)

In Δ AEF and Δ AGF,

⇒ ∠EAF = ∠GAF = 35° (AC being the bisector)

⇒ ∠AEF = ∠AGF = 40° (Proved above)

∴ Δ AEF ~ Δ AGF (By A.A. axiom)

Hence, proved that Δ AEF ~ Δ AGF.

(b) In Δ ACD,

⇒ ∠CAD = 35°

⇒ ∠ADC = 40°

By angle sum property of triangle,

⇒ ∠CAD + ∠ADC + ∠DCA = 180°

⇒ 35° + 40° + ∠DCA = 180°

⇒ ∠DCA + 75° = 180°

⇒ ∠DCA = 180° – 75° = 105°.

In Δ ACD and Δ ACB,

⇒ ∠ACB = ∠ACD = 105° (Proved above)

⇒ ∠BAC = ∠DAC = 35° (Proved above)

∴ Δ ACD ~ Δ ACB (By A.A. axiom)

(i) Given,

⇒ AE : EB = 2 : 3

Let AE = 2x and EB = 3x.

∴ AB = AE + EB = 2x + 3x = 5x.

We know that,

Ratio of corresponding sides are proportional.

\[\frac{AE}{AG}=\frac{AB}{AD}\\\Rightarrow\frac{AG}{AD}=\frac{AE}{AB}\\\Rightarrow\frac{AG}{AD}=\frac{2x}{5x}=\frac25\]

Hence, AG : AD = 2 : 5.

(ii) In △ ABC and △ ADC,

⇒ ∠BAC = ∠DAC (Both equal to 35°)

⇒ ∠ACB = ∠ACD (Both equal to 105°)

⇒ ∠ABC = ∠ADC (Both equal to 40°)

∴ △ ABC and △ ADC are congruent.

We know that,

Area of congruent triangles are equal.

Let area of △ ABC and area of △ ADC = x.

∴ Area of △ ABC : Area of △ ADC = x : x = 1 : 1.

Hence, area of △ ABC : area of △ ADC = 1 : 1.

(iii) From figure,

Area of quadrilateral ABCD = Area of △ ABC + Area of △ ADC = x + x = 2x.

∴ Area of quadrilateral ABCD : Area of △ ACB = 2x : x = 2 : 1.

Hence, area of quadrilateral ABCD : area of △ ACB = 2 : 1.

Question 102
In the given figure, angle ABC = 70° and angle ACB = 50°. Given, O is the centre of the circle and PT is the tangent to the circle. Then calculate the following angles

(a) ∠CBT

(b) ∠BAT

(d) ∠APT

Answer:

Join AT and BT.

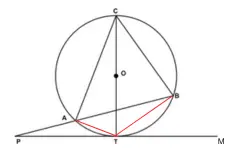
(a) We know that,

Angle in a semicircle is a right angle.

∴ ∠CBT = 90°.

Hence, ∠CBT = 90°.

(b) ∠CAT = 90° (Angle in a semicircle is a right angle.)

In △ABC,

⇒ ∠CBA + ∠CAB + ∠ACB = 180° [By angle sum property of triangle]

⇒ 70° + ∠CAB + 50° = 180°

⇒ ∠CAB + 120° = 180°

⇒ ∠CAB = 180° – 120°

⇒ ∠CAB = 60°.

From figure,

∠BAT = ∠CAT – ∠CAB = 90° – 60° = 30°.

Hence, ∠BAT = 30°.

∠BTM = ∠BAT = 30° [Angle in alternate segment]

∠PBT = ∠CBT – ∠CBA = 90° – 70° = 20°.

Hence, ∠PBT = 20°.

(d) ∠PTB = 180° – ∠BTX (linear pair)

= 180° – 30° = 150°.

In △PBT,

⇒ ∠PBT + ∠PTB + ∠APT = 180° [By angle sum property of triangle]

⇒ 20° + 150° + ∠APT = 180°

⇒ ∠APT + 170° = 180°

⇒ ∠APT = 180° – 170°

⇒ ∠APT = 10°

Hence, ∠APT = 10°

Question 103
(a) Construct a triangle ABC such that BC = 8 cm, AC = 10 cm and ∠ABC = 90°.

(b) Construct an incircle to this triangle. Mark the centre as I.

(d) Measure and write the length of the tangents from vertex C to the incircle.

(e) Mark points P, Q and R where the incircle touches the sides AB, BC, and AC of the triangle respectively. Write the relationship between ∠RIQ and ∠QCR.

(Use a ruler and a compass for this question.)

Answer:

Steps of construction :

Draw a line segment BC = 8 cm.

Draw BX perpendicular to BC.

With C as center and radius = 10 cm, draw an arc cutting BX at A.

Join AB and AC.

Draw BY and CZ the angle bisectors of B and C respectively.

Mark the point of intersection as I.

Draw IM perpendicular to side BC.

With I as center and radius IM draw a circle, which is the required incircle.

Mark points P, Q and R where the incircle touches the sides AB, BC, and AC of the triangle respectively.

Measure CQ and CR.

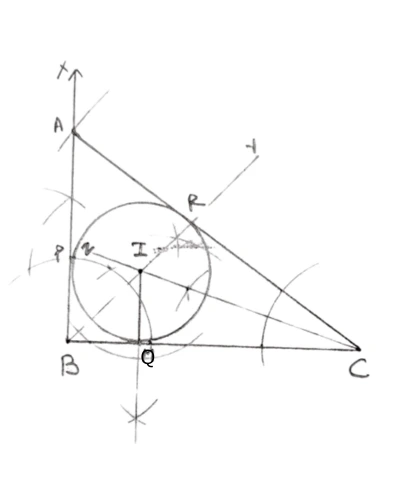
From figure,

⇒ ∠IQC = ∠IRC = 90° (The radius from the center of the circle to the point of tangency is perpendicular to the tangent line.)

⇒ ∠RCI = ∠QCI =∠C/2 (As CZ is angle bisector)

In △ IRC,

⇒ ∠RIC = 180° – ∠RCI – ∠IRC [∵ Sum of ∠’s in a Δ = 180°]

⇒ ∠RIC = 180° -∠C/2 – 90°

⇒ ∠RIC = 90° -∠C/2 …………(1)

In △ IQC,

⇒ ∠QIC = 180° – ∠IQC – ∠ICQ [∵ Sum of ∠’s in a Δ = 180°]

⇒ ∠QIC = 180° – 90° -∠C/2

⇒ ∠QIC = 90° – ∠C/2 …………(2)

Adding equations (1) and (2), we get :

⇒ ∠RIC + ∠QIC = 90° -∠C/2 + 90° -∠C/2

⇒ ∠RIQ = 180° – ∠C

⇒ ∠RIQ = 180° – ∠QCR

⇒ ∠RIQ + ∠QCR = 180°.

Hence, ∠RIQ + ∠QCR = 180°.

Question 104
The daily wages of workers in a construction unit were recorded as follows:

Class marks (Wages)	No. of workers
425	6
475	12
525	15
575	17
625	7
675	13

Form a frequency distribution table with class intervals and find modal wage by plotting a histogram.

Answer:

Difference between two consecutive class marks = 475 – 425 = 50.

Adjustment factor = Class width/2 = 50/2 = 25

Lower class limit = Class mark – Adjustment factor

Upper class limit = Class mark + Adjustment factor

Class marks (Wages)	No. of workers
400 – 450	6
450 – 500	12
500 – 550	15
550 – 600	17
600 – 650	7
650 – 700	13

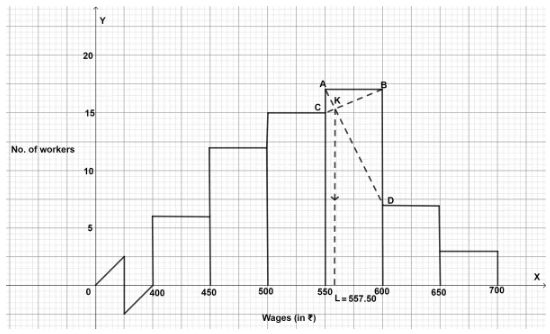
The daily wages of workers in a construction unit were recorded as follows

Let K be the point of intersection of AD and BC. From figure, mode= 557.50

Hence, mode = ₹ 557.50

Question 105
A bag contains 13 red cards, 13 black cards and 13 green cards. Each set of cards are numbered 1 to 13. From these cards, a card is drawn at random. What is the probability that the card drawn is a:

(a) green card?

(b) a card with an even number?

Answer:

Total no. of cards = 13 + 13 + 13 = 39 cards.

(a)

\[P\left(drawing\;a\;green\;card\right)=\frac{Number\;of\;green\;cards}{Total\;number\;of\;cards}\\\;\;=\frac{13}{39}=\frac13\]

(b) Even number cards are : 2, 4, 6, 8, 10, 12.

So, there are 6 even cards of each set i.e. 6 x 3 = 18 cards.

\[P\left(a\;card\;with\;an\;even\;number\right)=\frac{Number\;of\;even\;cards}{Total\;number\;of\;cards}\\\;\;=\frac{18}{39}=\frac6{13}\]

So, there are 4 cards of each red and black colour.

∴ 4 x 2 = 8 cards.

\[P\left(\;a\;red\;or\;black\;card\;with\;a\;number\;multiple\;of\;3\right)\\=\frac{red\;or\;black\;cards\;with\;a\;number\;multiple\;of\;3}{Total\;number\;of\;cards}\\\;\;=\frac8{39}\]

Competency Focused Questions – Multiple Choice Questions

Competency Focused Questions-Short Answer Questions-1

Competency Focused Questions- Long Answer Questions-1 (Graph based)

Competency Focused Questions – Long Answer Questions-2