ICSE Class 10 Mathematics Competency Focused Practice Questions Solution-Short Answer Questions 1

ICSE Class 10 Mathematics Competency Focused Practice Questions Solution

Short Answer Questions-1 (3 Marks Each)

Question 50
A shopkeeper marked a pressure cooker at ₹1800. The rate of GST on pressure cooker is 12%. The customer has only ₹1792 with him and he requests the shopkeeper to reduce the price so that he can buy the cooker in ₹1792. What percent discount must the shopkeeper give ?

Answer:

M.P. of pressure cooker = ₹1800

Let after discount the price of cooker be ₹ x.

GST on pressure cooker = 12%

According to the problem,

\[x+12\%of\;x=1792\\x+\frac{12x}{100}=1792\\\frac{112x}{100}=1792\\x=\frac{1792×100}{112}\\x=₹1600\\\therefore Discount\;=\;₹1800-₹1600=₹200\\Discount\%=\frac{discount}{M.P.}x100\\\;\;=\;\frac{200}{1800}x100\\\;\;=\;11.11\%\\Hence,\;discount\;given\;by\;the\;shopkeeper\;is\;11.11\%.\]

Question 51
A man opened a recurring deposit account in a branch of PNB. The man deposits certain amount of money per month such that after 2 years, the interest accumulated is equal to his monthly deposits. Find the rate of interest per annum that the bank was paying for the recurring deposit account.

Answer:

Given,

Time (n) = 2 years= 24 months

Rate = r%

Monthly installment (P) = ₹ x

Interest (I) = ₹ x

Using formula,

\[I=P\times\frac{n(n+1)}{2\times12}\times\frac r{100}\\\\x=x\times\frac{24\times25}{2\times12}\times\frac r{100}\\\frac r{100}=\frac{2\times12}{24\times25}\\r=4\%\\\]

Hence, rate of interest = 4%.

Question 52
Akshay buys 350 shares of ₹50 par value of a company. The dividend declared by the company is 14%. If his return percent from the shares is 10%, find the market value of each share.

Answer:

\[Return\%=\frac{income\;from\;1\;share}{Investment\;on\;1\;share}\times100\\Return\%=\frac{r\%\;of\;N.V.}{M.V.}\times100\\10\%=\frac{14\%\;of\;50}{M.V.}\times100\\M.V.=\;\frac{7\times100}{10}=₹\;70\]

Hence, market value of each share = ₹ 70.

Question 53
Solve the following inequation and answer the questions given below.

\[\frac12(2x-1)\leq2x+\frac12\leq5\frac12+x\]

(a) Write the maximum and minimum values of x for x ∈ R.

(b) What will be the change in maximum and minimum values of x if x ∈ W.

Answer: (a)

\[Given,\;\frac12(2x-1)\leq2x+\frac12\leq5\frac12+x\\Solving,\;\frac12(2x-1)\leq2x+\frac12\\\Rightarrow\frac{2x-1}2\leq\frac{4x+1}2\\\Rightarrow2x-1\leq4x+1\\\Rightarrow2x-4x\leq1+1\\\Rightarrow-2x\leq2\\\Rightarrow2x\geq-2\\\Rightarrow x\geq-1\\Now\;solving,\;2x+\frac12\leq5\frac12+x\\\Rightarrow\frac{4x+1}2\leq\frac{11}2+x\\\Rightarrow\frac{4x+1}2\leq\frac{11+2x}2\\\Rightarrow4x+1\leq11+2x\\\Rightarrow4x-2x\leq11-1\\\Rightarrow2x\leq10\\\Rightarrow x\leq5\]

If x ∈ R, then minimum value of x = -1 and maximum value of x = 5.

(b) x ∈ W then, minimum value of x = 0 and maximum value of x = 5.

Question 54

\[Solve\;for\;x,\;if\;\;\frac5x+4\sqrt3=\frac{2\sqrt3}{x^2},x\neq0\\\]

Answer:

\[\;\frac5x+4\sqrt3=\frac{2\sqrt3}{x^2}\\\Rightarrow\frac{5+4\sqrt3x}x=\frac{2\sqrt3}{x^2}\\\Rightarrow5+4\sqrt3x=\frac{2\sqrt3}x\\\Rightarrow5x+4\sqrt3x^2=2\sqrt3\\\Rightarrow4\sqrt3x^2+5x-2\sqrt3=0\\\Rightarrow4\sqrt3x^2+8x-3x-2\sqrt3=0\\\Rightarrow4x(\sqrt3x+2)-\sqrt3(\sqrt3x+2)=0\\\Rightarrow(\sqrt3x+2)(4x-\sqrt3)=0\\Either\;(\sqrt3x+2)=0\;or\;(4x-\sqrt3)=0\\So,\;Either\;x\;=\;\frac{-2}{\sqrt3}or\frac{\sqrt3}4\\\]

Question 55
The marked price of a toy is same as the percentage of GST that is charged. The price of the toy is ₹ 24 including GST. Taking the marked price as x, form an equation and solve it to find x.

Answer:

Given,

M.P. of toy = ₹ x

G.S.T. charged = x%

Price including G.S.T. = ₹ 24

\[\therefore x+x\%\;of\;x\;=\;24\\\Rightarrow x+\frac{x^2}{100}=24\\\Rightarrow\frac{100x+x^2}{100}=24\\\Rightarrow x^2+100x=2400\\\Rightarrow x^2+100x-2400=0\\\Rightarrow x^2+100x-2400=0\\\Rightarrow x^2+120x-20x-2400=0\\\Rightarrow x(x+120)-20(x+120)=0\\\Rightarrow(x+120)(z-20)=0\\Either\;(x+120)=0\;or\;(x-20)=0\\Either\;x=-120\;or\;20\\\]

Since, M.P. cannot be negative.

∴ M.P. = ₹20 and G.S.T. = 20%.

Hence, the marked price of toy = ₹ 20 and G.S.T. = 20%.

Question 56
The mean proportion between two numbers is 6 and their third proportion is 48. Find two numbers.

Answer:

Let the two numbers be a and b.

Given,

Mean proportion between the numbers is 6.

∴ a : 6 : : 6 : b

⇒ a : 6 = 6 : b

⇒ ab = 36

⇒ a = 36 / b ……… (1)

Third proportion of the numbers is 48.

∴ a : b : : b : 48

⇒ a : b = b : 48

⇒ b² = 48a ……….. (2)

Substituting the value of a in equation (2), we get:

b² = 48 x 36/b

⇒ b³ = 48 x 36

⇒ b = ∛48 x 36

⇒ b = ∛2 x2 x 2 x 2 x 3 x 2 x 2 x 3 x 3

⇒ b = 2 x 2 x 3

⇒ b = 12

Substituting the value of b in equation (1), we get :

⇒ a = 36/12

⇒ a = 3.

Hence, the numbers are 3 and 12.

Question 57
Pamela factorized the following polynomial:

2x³ + 3x² – 3x – 2

She found the result as (x + 2)(x – 1)(x – 2). Using remainder and factor theorem, verify whether her result is correct. If incorrect, give the correct result.

Answer:

Dividing the polynomial f(x) = 2x³ + 3x² – 3x – 2 by (x + 2), we get :

⇒ x + 2 = 0

⇒ x = -2

f(-2) = 2(-2)³ + 3(-2)² – 3(-2) – 2

= 2(-8) + 3(4) + 6 – 2

= -16 + 12 + 6 – 2

= -18 + 18

= 0.

Dividing the polynomial f(x) = 2x³ + 3x² – 3x – 2 by (x – 1), we get :

⇒ x – 1 = 0

⇒ x = 1

f(1) = 2(1)³ + 3(1)² – 3(1) – 2

= 2(1) + 3(1) – 3 – 2

= 2 + 3 – 3 – 2

= 0.

Dividing the polynomial f(x) = 2x³ + 3x² – 3x – 2 by (x – 2), we get :

⇒ x – 2 = 0

⇒ x = 2

f(2) = 2(2)³ + 3(2)² – 3(2) – 2

= 2(8) + 3(4) – 6 – 2

= 16 + 12 – 6 – 2

= 20.

Since, f(2) ≠ 0

∴ x – 2 does not divide the polynomial 2x³ + 3x² – 3x – 2. Her result is incorrect.

To get the correct result, we divide polynomial f(x) by (x + 2)(x – 1) or by (x² + x – 2):

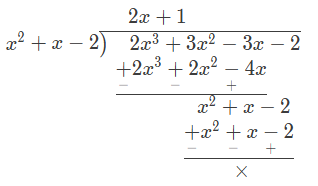
∴ 2x³ + 3x² – 3x – 2 = (x² + x – 2)(2x + 1)

= (x + 2)(x – 1)(2x + 1).

Hence, 2x³ + 3x² – 3x – 2 = (x + 2)(x – 1)(2x + 1).

Question 58

\[A=\begin{bmatrix}-6&0\\4&2\end{bmatrix}\;and\;B=\begin{bmatrix}1&0\\1&3\end{bmatrix}\\Find\;matrix\;M\;if,\\M=\frac12A-2B+5I,\;where\;I\;is\;the\;identity\;matrix.\]

Answer:

\[Given,\;M=\frac12A-2B+5I\\\Rightarrow M=\frac12\begin{bmatrix}-6&0\\4&2\end{bmatrix}-2\begin{bmatrix}1&0\\1&3\end{bmatrix}+5\begin{bmatrix}1&0\\0&1\end{bmatrix}\\\Rightarrow M=\begin{bmatrix}-3&0\\2&1\end{bmatrix}-\begin{bmatrix}2&0\\2&6\end{bmatrix}+\begin{bmatrix}5&0\\0&5\end{bmatrix}\\\Rightarrow M=\begin{bmatrix}-3-2+5&0-0+0\\2-2+0&1-6+5\end{bmatrix}\\\Rightarrow M=\begin{bmatrix}0&0\\0&0\end{bmatrix}\]

Question 59
(a) Write the nth term (T_n) of an Arithmetic Progression (A.P.) consisting of all whole numbers which are divisible by 3 and 7.

(b) How many of these are two-digit numbers? Write them.

Answer:

(a) A.P. consisting of all whole numbers which are divisible by 3 and 7= 21, 42, 63, ………

Here, first term (a) = 21 and common difference (d) = 42 – 21= 21.

By formula,

T_n = a + (n – 1)d

= 21 + (n – 1)21

= 21 + 21n – 21

= 21n.

Hence, the nth term = 21n.

(b) A.P. = 21, 42, 63, 84, 105, ……..

Hence, there are four two digit numbers i.e. 21, 42, 63, 84 in the A.P.

\[S_n=\frac n2\left\{2a+(n-1)d\right\}\\S_{10}=\frac{10}2\left\{2\times21+(10-1)21\right\}\\S_{10}=5\left\{42+189\right\}\\S_{10}=5\times231\\S_{10}=1155\]

Hence, sum of first 10 terms of the A.P. = 1155.

Question 60
Write the first five terms of the sequence given by (√3)ⁿ , n ∈ N

(a) Is the sequence an A.P. or G.P.?

(b) If the sum of its first ten terms is p(3 + √3), find the value of p.

Answer:

(a) Terms of the sequence given by(√3)ⁿ are:

(√3)¹ ,(√3)² ,(√3)³ ,(√3)⁴ ,(√3)⁵.

=√3, 3, 3√3, 9, 9√3

Ratio between the terms= 3/√3 = √3

Hence the terms are in G.P.

(b) By formula,

\[In\;G.P.\\S_n=\frac{a.(r^n-1)}{(r-1)}\\S_{10}=\frac{a.(r^{10}-1)}{(r-1)}\\p(3\;+\;\surd3)=\frac{\sqrt3.(\sqrt3^{10}-1)}{(\sqrt3-1)}\\p=\frac{\sqrt3.(243-1)}{(\sqrt3-1)(3\;+\;\surd3)}\\p=\frac{242\sqrt3}{3\sqrt3-3+3-\sqrt3}\\p=\frac{242\sqrt3}{2\sqrt3}\\p=121\\\]

Hence, p = 121.

Question 61
ABC is a triangle as shown in the figure below.

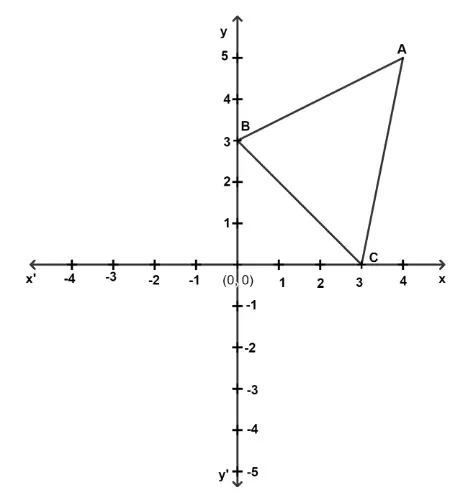
icse-class-10-mathematics-competency-focused-practice-questions-solution

(a) Write down the coordinates of A, B and C on reflecting through the origin.

(b) Write down the coordinates of the point/s which remain invariant on reflecting the triangle ABC on the x-axis and y-axis respectively.

Answer:

(a) From figure,

Coordinates of A= (4, 5). B= (0, 3) and C= (3, 0).

On reflecting in origin A, B and C becomes A’, B’ and C’.

Coordinates of A’ = (-4, -5), B’ = (0, -3) and C’ = (-3, 0).

(b) Point C(3, 0) lies on x-axis.

∴ It remains invariant on reflecting in x-axis.

Point B(0, 3) lies on y-axis.

∴ It remains invariant on reflecting in y-axis.

Hence, the invariant point for x-axis is point C and for y-axis is point B.

Question 62
Determine the ratio in which the line y = 2 + 3x divides the line segment AB joining the points A(-3, 9) and B(4, 2).

Answer:

By two point formula,

Equation of line :

\[y-y_1=\frac{y_2-y_1}{x_2-x_1}(x-x_1)\;(-3,9)(4,2)\\\Rightarrow y-9=\frac{2-9}{4+3}(x+3)\\\Rightarrow y-9=\frac{-7}7(x+3)\\\Rightarrow y-9=-1(x+3)\\\Rightarrow y-9=-x-3\\\Rightarrow x+y=6\\Solving\;equation\;y\;=\;2\;+\;3x\;and\;x\;+\;y\;=\;6\;simul\tan eously,\\3x-y=-2\;…….\;(1)\\x+y=6\;……\;(2)\\Adding\;the\;two\;equations,\;we\;get:\\4x=4\\x=1\\Substituting\;the\;value\;of\;x\;in\;equation\;(2)\;we\;get:\\1+y=6\\y=5\\Let\;(1,\;5)\;divide\;the\;line\;AB\;in\;the\;ratio\;k\;:\;1.\;\;\\By\;section\;formula,A(-3,\;9)\;and\;B(4,\;2).\\(x,y)=\left(\frac{mx_2+nx_1}{m+n},\frac{my_2+ny_1}{m+n}\right)\\(1,5)=\left(\frac{k\times4+1\times(-3)}{k+1},\frac{k\times2+1\times9}{k+1}\right)\\(1,5)=\left(\frac{4k-3}{k+1},\frac{2k+9}{k+1}\right)\\1=\frac{4k-3}{k+1}\\4k-3=k+1\\3k=4\\k=\frac43\\\therefore Ratio=\;4:3\\\]

Hence, the line y = 2 + 3x divides the line segment AB in the ratio 4 : 3.

Question 63
Square ABCD lies in the third quadrant of a XY plane such that its vertex A is at (-3, -1) and the diagonal DB produced is equally inclined to both the axes. The diagonals AC and BD meets at P(-2, -2). Find the :

(a) Slope of BD

(b) equation of AC

Answer:

(a) Given,

BD is equally inclined to both axes.

∴ Slope of BD = tan 45° = 1.

Hence, slope of BD = 1.

(b) Since, diagonals of a square are perpendicular and product of slope of perpendicular lines equals to -1.

∴ Slope of BD × Slope of AC = -1

⇒ 1 × Slope of AC = -1

⇒ Slope of AC = -1.

Since, diagonals meet at point (-2, -2).

By point-slope formula,

⇒ y – y₁ = m(x – x₁)

⇒ y – (-2) = -1[x – (-2)]

⇒ y + 2 = -1[x + 2]

⇒ y + 2 = -x – 2

⇒ x + y + 2 + 2 = 0

⇒ x + y + 4 = 0.

Hence, equation of AC is x + y + 4 = 0.

Question 64
ABCD is a rectangle where side BC is twice side AB. If △ACQ ~ △BAP, find area of △BAP : area of △ACQ.

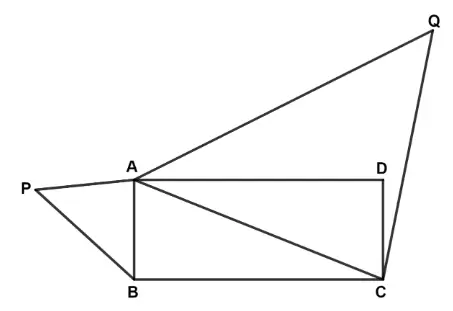
Answer:

Given,

ABCD is a rectangle where side BC is twice side AB.

⇒ BC = 2AB

In right angled triangle ABC,

By pythagoras theorem,

⇒ AC²= AB²+ BC²

⇒ AC² = AB² + (2AB)²

⇒ AC² = AB² + 4AB²

⇒ AC² = 5AB²

⇒ AC = √5AB.

We know that,

The ratio of the area of two similar triangles is equal to the square of the ratio of any pair of the corresponding sides of the similar triangles.

\[y-y_1=\frac{y_2-y_1}{x_2-x_1}(x-x_1)\;(-3,9)(4,2)\\\Rightarrow y-9=\frac{2-9}{4+3}(x+3)\\\Rightarrow y-9=\frac{-7}7(x+3)\\\Rightarrow y-9=-1(x+3)\\\Rightarrow y-9=-x-3\\\Rightarrow x+y=6\\Solving\;equation\;y\;=\;2\;+\;3x\;and\;x\;+\;y\;=\;6\;simul\tan eously,\\3x-y=-2\;…….\;(1)\\x+y=6\;……\;(2)\\Adding\;the\;two\;equations,\;we\;get:\\4x=4\\x=1\\Substituting\;the\;value\;of\;x\;in\;equation\;(2)\;we\;get:\\1+y=6\\y=5\\Let\;(1,\;5)\;divide\;the\;line\;AB\;in\;the\;ratio\;k\;:\;1.\;\;\\By\;section\;formula,A(-3,\;9)\;and\;B(4,\;2).\\(x,y)=\left(\frac{mx_2+nx_1}{m+n},\frac{my_2+ny_1}{m+n}\right)\\(1,5)=\left(\frac{k\times4+1\times(-3)}{k+1},\frac{k\times2+1\times9}{k+1}\right)\\(1,5)=\left(\frac{4k-3}{k+1},\frac{2k+9}{k+1}\right)\\\therefore\frac{Area\;of\;\bigtriangleup BAP}{Area\;of\;\bigtriangleup ACQ}=\left(\frac{AB}{AC}\right)^2\\\frac{Area\;of\;\bigtriangleup BAP}{Area\;of\;\bigtriangleup ACQ}=\left(\frac1{\sqrt5}\right)^2\\\frac{Area\;of\;\bigtriangleup BAP}{Area\;of\;\bigtriangleup ACQ}=\frac15\\\]

Hence, Area of △BAP : Area of △ACQ = 1 : 5.

Question 65
Given a triangle ABC, and D is a point on BC such that BD = 4 cm and DC = x cm. If ∠BAD = ∠C and AB = 8 cm, then,

(a) prove that triangle ABD is similar to triangle CBA.

(b) find the value of ‘x’.

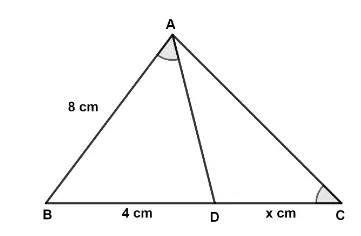
Answer:

(a) In △ ABD and △ CBA,

⇒ ∠ABD = ∠CBA (Common angle)

⇒ ∠BAD = ∠ACB (Given)

∴ △ ABD ~ △ CBA (By A.A. axiom)

Hence, proved that △ ABD ~ △ CBA.

(b) We know that,

Corresponding sides of similar triangle are proportional.

\[\therefore\frac{BD}{AB}=\frac{AB}{BC}\\\Rightarrow\frac48=\frac8{4+x}\\\Rightarrow16+4x=64\\\Rightarrow4x=64-16\\\Rightarrow4x=48\\\Rightarrow x=\frac{48}4=12\]

Hence, x = 12 cm.

Question 66
In the extract of Survey of India map G43S7, prepared on a scale of 2 cm to 1 km, a child finds the length of the cart track between two settlements is 7.6 cm. Find :

(a) the actual length of the cart track on the ground.

(b) actual area of a grid square, if each has an area of 4 cm².

Answer:

Scale factor (k) = 2 cm to 1 km or 2 cm to 100000 cm

= 2 : 100000 = 1 : 50000

(a) Length of cart track on ground = k × Length of cart track on map

Length of cart track on ground = 7.6 × 50000 = 380000 cm =3.8 km

Hence, length of actual cart track on ground = 3.8 km

(b) Area of actual grid square = k²× Area of model grid square

⇒ Area of actual grid square = (50000)² × 4

⇒ Area of actual grid square = 2500000000 × 4

⇒ Area of actual grid square =10000000000 cm² = 1 km² (100000 cm = 1km)

Hence, actual area of a grid square = 1 km².

Question 67
Construct a triangle ABC such that AB = 7 cm, BC = 6 cm and CA = 5 cm.

(a) Draw the locus of the points such that

(i) it is equidistant from BC and BA.

(ii) it is equidistant from points A and B.

(b) Mark P where the loci (i) and (ii) meet, measure and write length of PA.

Answer:

We know that,

Locus of the points equidistant from two sides is the angle bisector between two sides.

Locus of the points equidistant from two points is the perpendicular bisector of the line joining two points.

Steps of construction :

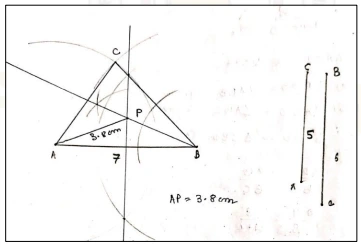
Draw a line segment AB = 7 cm.

With A and B as center and radii 5 cm and 6 cm respectively draw arcs intersecting at C.

Join AC and BC.

Draw BD, angle bisector of B.

Draw XY perpendicular bisector of AB.

Mark point P, the intersection point of XY and BD.

Measure AP.

Hence, AP = 3.8 cm.

Question 68
In the given figure O is the centre of the circle. ABCD is a quadrilateral where sides AB, BC, CD and DA touch the circle at E, F, G and H respectively. If AB = 15 cm, BC = 18 cm and AD = 24 cm, find the length of CD.

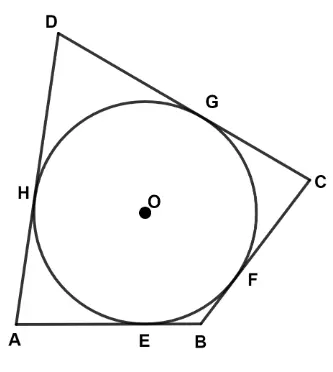
Answer:

We know that,

The length of tangents drawn from an external point to the circle are equal.

⇒ AE = AH = x (let)

⇒ BE = BF = y (let)

⇒ CF = CG = z (let)

⇒ DG = DH = m (let)

Given,

⇒ AB = 15

⇒ AE + EB = 15

⇒ x + y = 15 …….(1)

⇒ BC = 18

⇒ BF + CF = 18

⇒ y + z = 18 ……..(2)

⇒ AD = 24

⇒ AH + DH = 24

⇒ x + m = 24 ……….(3)

Adding equations (2) and (3), we get :

⇒ y + z + x + m = 18 + 24

⇒ x + y + z + m = 42

⇒ 15 + z + m = 42 [From (1)]

⇒ z + m = 42 – 15

⇒ z + m = 27.

⇒ CD = CG + DG = m + z = 27 cm.

Hence, length of CD = 27 cm.

Question 69
In the given diagram, ABCDEF is a regular hexagon inscribed in a circle with centre O. PQ is a tangent to the circle at D. Find the value of :

(a) ∠FAG

(b) ∠BCD

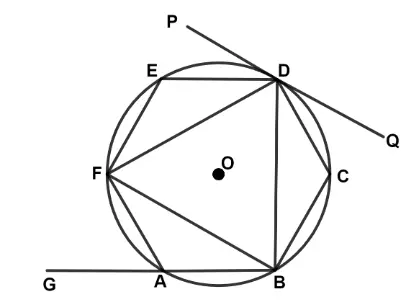
Answer:

(a) We know, Each interior angle of a regular hexagon =120°.

∴ ∠FAB = 120°

∠FAG + ∠FAB = 180° (linear pair)

∴ 120° + ∠FAG = 180°

⇒ ∠FAG = 180° – 120° = 60°.

Hence, ∠FAG = 60°.

(ii) Each interior angle of regular hexagon = 120°.

Hence, ∠BCD = 120°.

(iii) In △FED,

FE = DE (ABCDEF is a regular hexagon)

∴ ∠EFD = ∠EDF = x° (let)

Now, We know ∠FED = 120° (angle of a regular hexagon)

∴ ∠EFD + ∠FED + ∠EDF = 180° (angle sum property of a triangle)

⇒ x° + 120° + x° = 180°

⇒ 2x° = 180° – 120°

⇒ x° = 60/2 = 30°

We know that,

The angle between a tangent and a chord through the point of contact is equal to an angle in the alternate segment.

⇒ ∠PDE = ∠EFD = 30°.

Hence, ∠PDE = 30°.

Question 70
AB and CD intersect at the center O of the circle given in the above diagram. If ∠EBA = 33° and ∠EAC = 82°, find

(a) ∠BAE

(b) ∠BOC

Answer:

(a) In △ BAE,

⇒ ∠AEB = 90° (Angle in a semicircle is a right angle)

By angle sum property of triangle,

⇒ ∠AEB + ∠EBA + ∠BAE = 180°

⇒ 90° + 33° + ∠BAE = 180°

⇒ ∠BAE + 123° = 180°

⇒ ∠BAE = 180° – 123° = 57°.

Hence, ∠BAE = 57°.

(b) From figure,

⇒ ∠EAC = ∠EAB + ∠BAC

⇒ 82° = 57° + ∠BAC

⇒ ∠BAC = 82° – 57° = 25°.

We know that,

The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.

⇒ ∠BOC = 2∠BAC = 2 × 25° = 50°.

Hence, ∠BOC = 50°.

∠BOC and ∠BOD form a linear pair.

∴ ∠BOC + ∠BOD = 180°

⇒ 50° + ∠BOD = 180°

⇒ ∠BOD = 180° – 50° = 130°.

In △ BOD,

⇒ ∠BOD + ∠ODB + ∠DBO = 180°

⇒ 130° + ∠ODB + 33° = 180°

⇒ ∠ODB + 163° = 180°

⇒ ∠ODB = 180° – 163° = 17°.

Hence, ∠ODB = 17°.

Question 71
A famous sweet shop “Madanlal Sweets” sells tinned rasgullas. The tin container is cylindrical in shape with diameter 14 cm, height 16 cm, and it can hold 20 spherical rasgullas of diameter 6 cm and sweetened liquid such that the can is filled and then sealed. Find out how much sweetened liquid the can contains. Take π = 3.14.

Answer:

Given,

Diameter of container = 14 cm

Radius (R) = 14/2 = 7 cm

Height of container (H) = 16 cm

Diameter of rasgulla = 6 cm

Radius of rasgulla (r) = 6/2 = 3 cm

Volume of container = Volume of rasgullas + Volume of liquid

⇒ πR²H = 20 x 4/3πr³ + Volume of liquid

⇒ Volume of liquid = πR²H -80/3πr³

⇒ Volume of liquid = π(R²H – 80/3 r³)

⇒ Volume of liquid = 3.14 × (7² × 16 – 80/3 × 3³)

⇒ Volume of liquid = 3.14 × (784 – 720)

⇒ Volume of liquid = 3.14 × 64

⇒ Volume of liquid = 200.96 cm³.

Hence, volume of sweetened liquid in the container = 200.96 cm³.

Question 72
The ratio of the radius and the height of a solid metallic right circular cylinder is 7 : 27. This is melted and made into a cone of diameter 14 cm and slant height 25 cm. Find the height of the :

(a) cone

(b) cylinder

Answer:

Given,

Diameter of cone = 14 cm

Radius of cone (r) = Diameter/2 = 14/2 = 7 cm

Slant height (l) = 25 cm

Ratio of the radius and the height of a solid metallic right circular cylinder is 7 : 27.

Let radius of cylinder (R) = 7x

and height of cylinder (H) = 27x

(a) Let height of cone be h cm.

By formula,

⇒ l2 = r² + h²

⇒ 25² = 7² + h²

⇒ 625 = 49 + h²

⇒ h² = 625 – 49

⇒ h² = 576

⇒ h = √576 = 24 cm.

Hence, height of cone = 24 cm.

(b) Given,

A solid metallic right circular cylinder is melted and made into a cone.

∴ Volume of cylinder = Volume of cone

⇒ πR²H = 1/3 πr²h

⇒ R²H = 1/3 r²h

⇒ (7x)² x 27x= 1/3 x 7² x 24

⇒ 49 x² x 27x = 49 x 8

⇒ 1323x³ = 392

⇒ x³ = 392/1323

⇒ x³ = 8/27

⇒ x = ∛8/27
= 2/3

Height of cylinder (H) = 27x = 27 × 2/3
= 18 cm.

Hence, height of cylinder = 18 cm.

Question 73
An inclined plane AC is prepared with its base AB which is √3 times its vertical height BC. The length of the inclined plane is 15 m. Find:

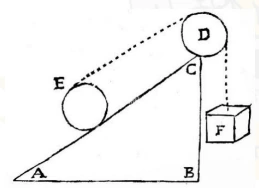
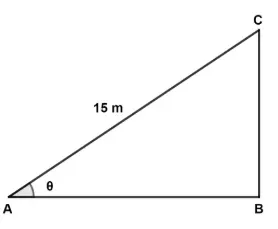
(a) value of θ.

(b) length of its base AB, in nearest metre.

Answer:

(a) According to question,

⇒ AB = √3 BC

\[Now,\;\tan\theta=\frac pb=\frac{BC}{AB}\\\tan\theta=\frac{BC}{\sqrt3BC}\\\tan\theta=\frac1{\sqrt3}\\\tan\theta=\tan\;30^\circ\\\theta=30^\circ\\\]

Hence, θ = 30°.

(b) In right angle triangle ABC,

By pythagoras theorem,

⇒ AC² = BC² + AB²

⇒ 15² = BC² + (√3BC)²

⇒ 225 = BC² + 3BC²

⇒ 225 = 4BC²

⇒ BC² = 225/4

⇒ BC = √225/4

⇒ BC = 15/2 = 7.5 cm

∴ AB = √3 BC = √3 x 7.5

⇒ AB = 1.732 x 7.5

⇒ AB = 12.99 m

⇒ AB = 13 m (round off)

Hence, AB = 13 m.

Question 74
Prove that :

tan² θ + cos² θ – 1 = tan² θ. sin²θ

Answer

Solving L.H.S. we get:

\[\tan^2\theta+\cos^2\theta-1\\\Rightarrow\frac{\sin^2\theta}{\cos^2\theta}+\cos^2\theta-1\\\Rightarrow\frac{\sin^2\theta+\cos^4\theta-\cos^2\theta}{\cos^2\theta}\\\Rightarrow\frac{1-\cos^2\theta+\cos^4\theta-\cos^2\theta}{\cos^2\theta}\\\Rightarrow\frac{1-2\cos^2\theta+\cos^4\theta}{\cos^2\theta}\\\Rightarrow\frac{{(1-\cos^2\theta)}^2}{\cos^2\theta}\\\Rightarrow\frac{{(\sin^2\theta)}^2}{\cos^2\theta}\\\Rightarrow\frac{\sin^2\theta\;.\;\sin^2\theta\;\;}{\cos^2\theta}\\\Rightarrow\frac{\sin^2\theta\;\;}{\cos^2\theta}\times\;\sin^2\theta\;\;\\\Rightarrow\tan^2\theta\;.\;\sin^2\theta\;\;=\;R.H.S.\\Hence\;Proved.\\\\\\\]

Question 75
The class mark and frequency of a data is given in the graph. From the graph, Find:

(a) the table showing the class interval and frequency.

(b) the mean

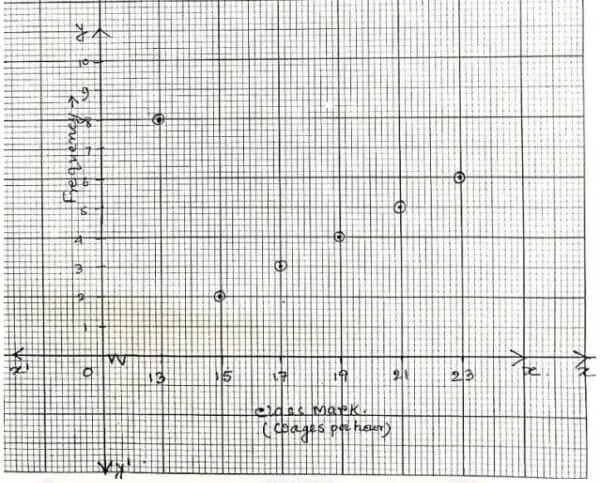
Answer:

(a) Class marks : 13, 15, 17, 19, 21, 23.

Difference between two consecutive class marks = 15 – 13 = 2.

Lower limit of class = Class mark – 1

Upper limit of class = Class mark + 1

Class	Frequency
12 – 14
14 – 16
16 – 18
18 – 20
20 – 22

(b)

Class	Class mark (x)	frequency (f_i)	f_i x_i
12 – 14	13	8	104
14 – 16	15	2	30
16 – 18	17	3	51
18 – 20	19	4	76
20 – 22	21	5	105
22 – 24	23	6	138
	Total	Σf_i = 28	Σf_i x_i = 504

Mean = Σf_i x_i /Σf_i
= 504/28
= 18

Hence, mean = 18.

Question 76
The mean of 5, 7, 8, 4 and m is n and the mean of 5, 7, 8, 4, m and n is m. Find the values of m and n.

Answer:

\[Given,\\n=\frac{5+7+8+4+m}5\\5n=24+m\\m=5n-24\;……\;(1)\\\\m=\frac{5+7+8+4+m+n}6\\6m=24+m+n\\5m=24+n\\n=5m-24\\putting\;the\;value\;of\;m\;from\;(1),\;we\;get\\n=5(5n-24)-24\\n=25n-120-24\\25n-n=120+24\\24n=124\\n=\frac{124}{24}\\n=6\\Putting\;n=6\;in\;equation\;(1),\;we\;get,\\m=5\times6-24\\m=30-24=6\\\]

Hence, m = 6 and n = 6.

Question 77
The probability of selecting a blue marble and a red marble from a bag containing red, blue and green marbles is 1/3 and 1/5 respectively. If the bag contains 14 green marbles, then find :

(a) number of red marbles.

(b) total number of marbles in the bag.

Answer:

(b) As the bag contains red, blue and green marbles.

∴ Probability of selecting a red marble + Probability of selecting a blue marble + Probability of selecting a green marble = 1

⇒ 1/3 + 1/5 + P(green marble)= 1

⇒ P(green marble) = 1 – 1/3 – 1/5

⇒ P(green marble) = (15-5-3)/15

⇒ P(green marble) = 7/15

Let total number of marbles in the bag be x.

No. of green marbles = 14

∴ 14/x = 7/15