ICSE Maths Competency Based Questions Solution
Long Answer Questions 2 (5 Marks Each)
Question 110
On seeing the below display board outside Pearl Stationary Shop, Chetan enters the shop to buy the following items:

| Pen | Pencil | Rainbow cover notebook | |
| Price | ₹5 each | ₹7 each | ₹200 each |
| Discount | 5% on a dozen pens | 10% on 20 pencils | – |
| Premium | – | – | ₹50 on each notebook |
| Items purchased | 1 dozen | 20 pencils | 5 |
| GST | 18% | 12% | 12% |
The shopkeeper handed over the bill to Chetan saying that he has given further discount of 2% on total bill. Chetan became so happy hearing about the discount that he did not check the bill until he reached home. He later found out that though shopkeeper has given 2% discount as promised, he had also mischarged uniform 18% GST on all the items.
(a) Calculate :
(i) total selling price of all the items as per the offers displayed on the board.
(ii) total amount to be paid by Chetan including GST with correct rates.
(iii) actual amount charged by the shopkeeper.
(b) Did the shopkeeper overcharge Chetan? Justify your answer
Answer:
(a)
| pen | Pencil | Notebook |
| No. of pens purchased= 12 Price of 12 pens= ₹5 × 12 = ₹60 Discount: 5% on dozen pens. =5% of ₹60 = ₹3 Price after discount = ₹60 – ₹3 = ₹57. GST = 18% = 18/100 x 57 = ₹10.26 Total price: ₹57 + ₹10.26 = ₹67.26 | No. of pencils purchased= 20 Price of 20 pencils= ₹7 × 20 = ₹140 Discount: 10% on 20 pencils. = 10% of ₹140 =₹14. Price after discount= ₹140 – ₹14 = ₹126. GST = 12% = 12% of ₹126 = ₹ 15.12 Total price: ₹126 + ₹15.12 = ₹141.12 | No. of notebooks purchased= 5 Price of 5 notebooks= ₹200 × 5 = ₹1000 Premium: ₹50 on each notebook Total premium: ₹50 × 5 = ₹250. Price after premium= ₹1000 + ₹250 = ₹1250 GST = 12% = 12% of ₹1250 = ₹150. Total price : ₹1250 + ₹150 = ₹1400 |
(i) Total selling price of all items = ₹57 + ₹126 + ₹1250 = ₹1433.
Hence, total selling price = ₹1433.
(ii) Total price paid (including GST) = ₹67.26 + ₹141.12 + ₹1400 = ₹1608.38
Hence, total price paid (including GST) = ₹1608.38
(iii) On applying incorrect GST rates:
| Pen | Pencil | Notebook |
| Price after discount = ₹57 GST = 18% = 18% of ₹57 = ₹10.26 Total price : ₹57 + ₹10.26 = ₹67.26 | Price after discount = ₹126. GST = 18% = 18% of ₹126 = ₹22.68 Total price : ₹126 + ₹22.68 = ₹148.68 | Price after premium = ₹1250. GST = 18% = 18% of ₹1250 = ₹225. Total price : ₹1250 + ₹225 = ₹1475. |
When the GST rate is applied as 18% uniformly, bill need to be paid by Chetan:
= ₹1475 + ₹148.68 + ₹67.26
= ₹1690.94
Discount given on total bill = 2%
= 2% of ₹1690.94
= ₹33.82
Bill = ₹1690.94 – ₹33.82 = ₹1657.12
Hence, bill = ₹1657.12
(b) The bill should be of ₹1608.38 but instead it was of ₹1657.12
⇒ Overcharge = ₹1657.12 – ₹1608.38 = ₹48.78
Hence, the shopkeeper overcharged an amount of ₹48.78
Question 111
Using remainder and factor theorem, show that (2x + 3) is a factor of the polynomial 2x2 + 11x + 12. Hence, factorise it completely. What must be multiplied to the given polynomial so that x2 + 3x – 4 is a factor of the resulting polynomial? Also, write the resulting polynomial.
Answer
2x + 3 = 0
⇒ 2x = -3
⇒ x = -3/2
Substituting value of x in equation 2x2 + 11x + 12, we get :
⇒ 2(-3/2)2 + 11(-3/2) + 12
⇒ 2 x9/4 -33/2 + 12
⇒ 9/2 – 33/2 + 12
⇒ (9 – 33 + 24)/2
⇒ -0/2 = 0
Since, remainder = 0.
∴ 2x + 3 is a factor of the polynomial 2x2 + 11x + 12.
Solving polynomial, 2x2 + 11x + 12, we get :
⇒ 2x2 + 8x + 3x + 12
⇒ 2x(x + 4) + 3(x + 4)
⇒ (2x + 3)(x + 4).
Solving polynomial, x2 + 3x – 4, we get :
⇒ x2 + 4x – x – 4
⇒ x(x + 4) – 1(x + 4)
⇒ (x – 1)(x + 4).
∴ (x – 1) and (x + 4) are factors of x2 + 3x – 4.
∴ On multiplying polynomial, 2x2 + 11x + 12 by (x – 1) it will be divisible by x2 + 3x – 4.
⇒ (2x2 + 11x + 12)(x – 1)
⇒ 2x3 – 2x2 + 11x2 – 11x + 12x – 12
⇒ 2x3 + 9x2 + x – 12.
Hence, the resulting polynomial = 2x3 + 9x2 + x – 12.
Question 112
The sequence 2, 9, 16, ….. is given.
(a) Identify if the given sequence is an AP or a GP. Give reasons to support your answer.
(b) Find the 20th term of the sequence.
(c) Find the difference between the sum of its first 22 and 25 terms.
(d) Is the term 102 belong to this sequence?
(e) If ‘k’ is added to each of the above terms, will the new sequence be in A.P. or G.P.?
Answer
(a) Difference between common terms : 16 – 9 = 9 – 2 = 7.
Since, common difference are equal.
Hence, the given sequence is an A.P.
(b) By formula,
an = a + (n – 1)d
a20 = 2 + (20 – 1) × 7
= 2 + 19 × 7
= 2 + 133
= 135.
Hence, 20th term of the sequence = 135.
(c)
S25 – S22 = 2150 – 1661 = 489.
Hence, difference between the sum of its first 22 and 25 terms = 489.
(d) Let nth term be 102.
⇒ an = a + (n – 1)d
⇒ 102 = 2 + 7(n – 1)
⇒ 102 = 2 + 7n – 7
⇒ 102 = 7n – 5
⇒ 102 + 5 = 7n
⇒ 7n = 107
⇒ n = 107/7
Since, n cannot be in fraction.
Hence, 102 is not the term of the sequence.
(e) If k is added to each term.
Sequence : 2 + k, 9 + k, 16 + k,………….
The common difference between terms is still equal to 7.
Hence, sequence is in A.P.
Question 113
Given the equations of two straight lines, L1 and L2 are x – y = 1 and x + y = 5 respectively. If L1 and L2 intersects at point Q (3, 2). Find :
(a) the equation of line L3 which is parallel to L1 and has y-intercept 3.
(b) the value of k, if the line L3 meets the line L2 at a point P (k, 4).
(c) the coordinate of R and the ratio PQ : QR, if line L2 meets x-axis at point R.
Answer
(a) Equation of L1 ⇒ x – y = 1
⇒ y = x – 1
Comparing above equation with y = mx + c, we get :
⇒ m = 1.
We know that,
Slope of parallel lines are equal.
∴ Slope of L3 = 1.
Given,
y-intercept of L3 = 3.
∴ y = mx + c
⇒ y = 1.x + 3
⇒ y = x + 3.
Hence, equation of line L3 is y = x + 3.
(b) Equation of L2 ⇒ x + y = 5
Equation of L3 ⇒y = x + 3
⇒ x + y = 5 ………(1)
⇒ y = x + 3 ………(2)
Substituting value of y from equation (2) in (1), we get :
⇒ x + (x + 3) = 5
⇒ 2x + 3 = 5
⇒ 2x = 5 – 3
⇒ 2x = 2
⇒ x = 1
Substituting value of x in equation (2), we get :
⇒ y = 1 + 3 = 4.
⇒ (x, y) = (1, 4)
∴ P(k, 4) = (1, 4)
Hence, value of k = 1.
(c) Given,
L2 meets x-axis at point R.
At point on x-axis, y-coordinate = 0.
Equation of L2 ⇒ x + y = 5
⇒ x + 0 = 5
⇒ x = 5
⇒ R = (x, y) = (5, 0).
P = (1, 4), Q = (3, 2) and R = (5, 0)
Let PQ : QR = k : 1
By section formula,
∴ PQ : QR = 1 : 1.
Hence, R = (5, 0) and PQ : QR = 1 : 1.
Question 114
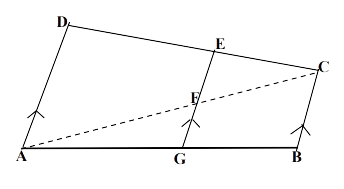
In the figure given below (not drawn to scale), AD ∥ GE ∥ BC, DE = 18 cm, EC = 3 cm, AD = 35 cm. Find :
(a) AF : FC
(b) length of EF
(c) area(trapezium ADEF) : area(Δ EFC)
(d) BC ∶ GF
Answer:
(a) In △ ACD and △ FCE,
⇒ ∠ACD = ∠FCE (Common angles)
⇒ ∠ADC = ∠FEC (Corresponding angles are equal)
∴ △ ACD ~ △ FCE (By A.A. axiom)
We know that,
Ratio of corresponding sides of similar triangle are proportional.
Let FC = x and AC = 7x.
From figure,
AF = AC – FC = 7x – x = 6x.
AF : FC = 6 : 1
Hence, AF : FC = 6 : 1.
(b) Since, △ ACD ~ △ FCE
Hence, EF = 5 cm.
(c) We know that,
The ratio of the area of two similar triangles is equal to the square of the ratio of any pair of the corresponding sides of the similar triangles.
Hence, area of trapezium ADEF : area of △ EFC = 48 : 1.
(d) In △ AGF and △ ABC,
⇒ ∠AGF = ∠ABC (Corresponding angles are equal)
⇒ ∠GAF = ∠BAC (Common angles)
∴ △ AGF ~ △ ABC (By A.A. axiom)
We know that,
Ratio of corresponding sides of similar triangle are proportional.
Hence, BC : GF = 7 : 6.
Question 115
(a) Construct the locus of a moving point which moves such that it keeps a fixed distance of 4.5 cm from a fixed-point O.
(b) Draw line segment AB of 6 cm where A and B are two points on the locus (a).
(c) Construct the locus of all points equidistant from A and B. Name the points of intersection of the loci (a) and (c) as P and Q respectively.
(d) Join PA. Find the locus of all points equidistant from AP and AB.
(e) Mark the point of intersection of the locus (a) and (d) as R. Measure and write down the length of AR.
(Use a ruler and a compass for this question.)
Answer:
We know that,
Locus of a point at a fixed distance from a fixed point is the circumference of the circle with fixed point as center and fixed distance as radius.
Steps of construction :
Mark point O.
With center O and radius = 4.5 cm draw a circle.
Use a ruler to mark point A.
From point A, measure 6 cm along a straight line and mark point B.
Draw a straight line connecting points A and B.
We know that, locus of points equidistant from two points is the perpendicular bisector of the line joining the two points.
Draw perpendicular bisector of AB.
Mark the points P and Q where the perpendicular bisector intersects circle.
We know that, locus of points equidistant from two lines is the angle bisector of the angle between the lines.
Join PA.
Draw AX, the angle bisector of ∠A.
Mark point R as the intersection point of AX on the circumference of the circle.
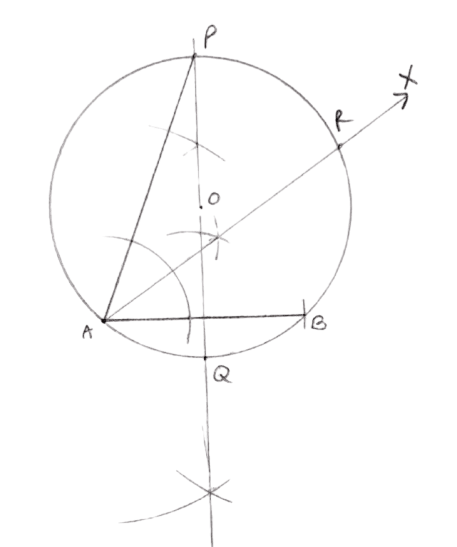
Measure AR.
Hence, AR ≈ 8.8 cm
Question 116
Construct a regular hexagon ABCDEF of side 4.3 cm and construct its circumscribed circle. Also, construct tangents to the circumscribed circle at points B and C which meets each other at point P. Measure and record ∠BPC.
(Use a ruler and a compass for this question.)
Answer:
We know that each angle in a regular hexagon = 120°.
Draw a line segment AB = 4.3 cm.
At A and B draw rays making an angle of 120° each and cut off AF = BC = 4.3 cm.
At F and C, draw rays making angle of 120° each and cut off EF = CD = 4.3 cm.
Join ED. Hence, ABCDEF is the required hexagon.
Draw the perpendicular bisector of AB and BC. Let these bisectors meet at the point O.
With O as center and radius equal to OA or OB draw a circle which passes through the vertices of the hexagon. This is the required circumcircle of hexagon ABCDEF.
Draw the radius OB and OC.
At point B, construct a line perpendicular to OB. This line is the tangent at B.
At point C, construct a line perpendicular to OC. This line is the tangent at C.
The two tangents will intersect at point P.
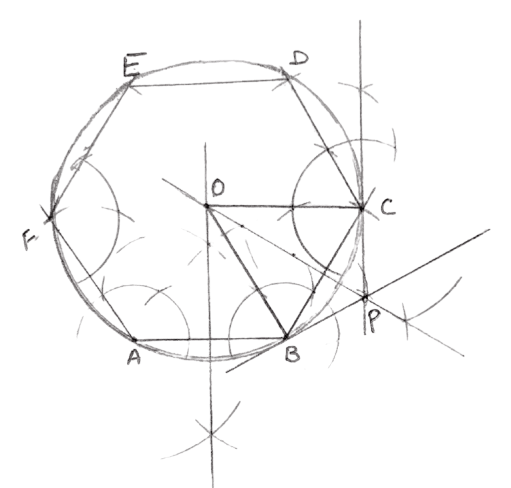
Measure ∠BPC.
Hence, ∠BPC = 120°.
Question 117
A mathematics teacher uses certain amount of terracotta clay to form different shaped solids. First, she turned it into a sphere of radius 7 cm and then she made a right circular cone with base radius 14 cm. Find the height of the cone so formed. If the same clay is turned to make a right circular cylinder of height 7/3 cm, then find the radius of the cylinder so formed. Also, compare the total surface areas of sphere and cylinder so formed.
Answer:
Let R be radius and h be height of right circular cone. Let r be the radius of the sphere.
As same amount of clay is used to make a sphere and then a right circular cone.
∴ Volume of cone = Volume of sphere
∴ Height of the right circular cone=7 cm
Given,
The same clay is used to make a right circular cylinder of height (h) 7/3 cm.
Let its radius be R.
Since same amount of clay is used to make cylinder and sphere.
∴ Volume of cylinder = Volume of sphere
Hence, radius of cylinder is 14 cm.
Total surface area of sphere = 4πr2
Total surface area of cylinder = 2πR(h + R)
Hence, height of cone = 7 cm, radius of cylinder = 14 cm and Total surface area of sphere : Total surface area of cylinder = 3 : 7.
Question 118
A tree (TS) of height 30 m stands in front of a tall building (AB). Two friends Rohit and Neha are standing at R and N respectively, along the same straight line joining the tree and the building (as shown in the diagram). Rohit, standing at a distance of 150 m from the foot of the building, observes the angle of elevation of the top of the building as 30°. Neha from her position observes that the top of the building and the tree has the same elevation of 60°.
Find the:
(a) height of the building
(b) distance between
(i) Neha and the foot of the building
(ii) Rohit and Neha
(iii) Neha and the tree
(iv) building and the tree.
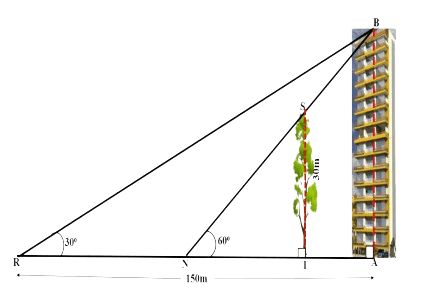
Answer:
(a) From figure,
Hence, height of the building = 86.6 m.
(b)
(i) From figure,
Hence, distance between Neha and foot of the building = 50 m.
(ii) From figure,
RN = AR – AN = 150 – 50 = 100 m.
Hence, distance between Rohit and Neha = 100 m.
(iii) From figure,
Hence, distance between Neha and the tree = 17.32 m.
(iv) From figure,
AT = AN – NT = 50 – 17.32 = 32.68 m
Hence, distance between building and tree = 32.68 m.
Question 119
A life insurance agent found the following data of age distribution of 100 policy holders, where f is an unknown frequency.
| Age in years | No. of policy holders |
| 15 – 20 | 7 |
| 20 – 25 | 12 |
| 25 – 30 | 15 |
| 30 – 35 | 22 |
| 35 – 40 | f |
| 40 – 45 | 14 |
| 45 – 50 | 8 |
| 50 – 55 | 4 |
(a) If the mean age of the policy holders is 35.65 years, find the unknown frequency f.
(b) Find the median class of the distribution.
Answer:
(a) Given,
Total no. of policy holders = 100
∴ 7 + 12 + 15 + 22 + f + 14 + 8 + 4 = 100
⇒ 82 + f = 100
⇒ f = 100 – 82 = 18.
Hence, f = 18.
(b) Cumulative frequency distribution table:
| Age in years | No. of policy holders (f) | Cumulative frequency (cu. f.) |
| 15 – 20 | 7 | 7 |
| 20 – 25 | 12 | 19 |
| 25 – 30 | 15 | 34 |
| 30 – 35 | 22 | 56 |
| 25 – 40 | 18 | 74 |
| 40 – 45 | 14 | 88 |
| 45 – 50 | 8 | 96 |
| 50 – 55 | 4 | 100 |
Since, n = 100, (even)
Median = n/2 th = 50th term.
Steps of construction :
Plotting the points (20, 7), (25, 19), (30, 34), (35, 56), (40, 74), (45, 88), (50, 96) and (55, 100) on graph and joining them free hand, we get:
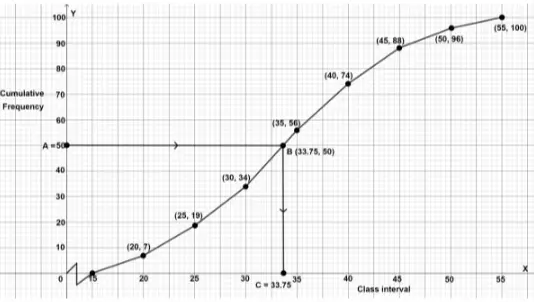
From graph,
Median= 50 th term= 33.75, which lies between 30-35.
Hence, median class = 30-35.
ICSE Related Links
Chapter-wise Quiz/MCQ/Test:
ICSE Chapter wise Quiz For Class 6
ICSE Chapter wise Quiz For Class 7
ICSE Chapter wise Quiz For Class 8
ICSE Chapter wise Quiz For Class 9
ICSE Chapter wise Quiz For Class 10
Sample Papers
Board Papers
ICSE Class 9 Board Exam Papers
ICSE Class 10 Board Exam Papers
CBSE Related Links
Chapter wise Quiz/MCQ/Test
CBSE Chapter-wise Quiz for Class 6
CBSE Chapter-wise Quiz for Class 7
CBSE Chapter-wise Quiz for Class 8
CBSE Chapter-wise Quiz for Class 9
CBSE Chapter-wise Quiz for Class 10
Sample Papers
Board Papers
CBSE Class 10 Previous years’ Board Papers
Subscribe to our YouTube channel for more educational content.

